Я понимаю, что их четыре и они именно такие. Но допустим я определю два отображения:
Пусть

,

.
Обозначим

,

,
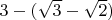
,

. Тогда с помощью данных отображений я могу тасовать все корни:





То есть получается, что группа Галуа состоит из элементов:

?. Имеем четыре элемента в группе Галуа. Если я правильно понимаю определение прямой суммы, то данная группа изоморфна двум группам порядка 2, ибо

как раз дает 4, то есть каждый элемент определен однозначно. Так ведь?