Очевидно, что подобного рода уравнение может описывать основные состояния более-менее адекватно -- если только, конечно, много-много уровней лежат вблизи дна той ямы из перевёрнутых косинусов.
Это же самое выражается формулой
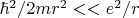
- это неравенство позволяет пользоваться квадратичным разложением.
Если ТС теперь выразит

через параметры уравнения и воспользуется неравнеством написанным выше, то сможет убедиться, что

что позволяет протянуть пределы до бескнечности в интеграле. (Если, конечно, он подразумевает

это тот самый угол, что в уравнении)