Brukvalub писал(а):
Тогда еще раз подумайте над этим:
Brukvalub писал(а):
Чтобы выделить ветвь, нужно тем или иным способом запретить возможность обхода вокруг точек ветвления, например, проведя разрез - луч с началом в нуле, проходящий через вторую точку ветвления.
Если я правильно понимаю, что происходит, то для этого мне данно условие

?
Brukvalub писал(а):
Ведь речь-то идет о функции

, а ветвь Вы выделяете у функции

. Первая из функций имеет больше точек ветвления!
Так мне же сказанно в условие

а не
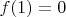
.
Brukvalub писал(а):
И еще: почему бы Вам не разложить сумму z+z^2 на множители , после чего привлечь алгебраические свойства логарифма?
Опять таки я все время думал, чтобы привлечь свойства логарифма нужно сначала определиться с веткой.
RIP писал(а):
Смотрите, у Вас есть функция

, где

- многозначная функция,

. Главная ветвь функции

выделяется в области

Так вот, когда точка

бегает по интересующему Вас множеству (окружность), точка

совершает полный круг вокруг точки ветвления
(

) логарифма, поэтому заведомо произойдет смена ветви.
Так мое множество не полная окружность?
RIP писал(а):
Ветвь

(главное значение аргумента) не будет непрерывна на интересующем Вас множестве.
А откуда это видно мне до сих пор не ясно.
Хорошо у меня появилась другая идея на почве полного отчаяния. А если я для начала посматрю на трансформацию окружности с помощью

, а потом то что получилось прогоню через

. Но опять таки не ясно с веткой.