Нестандартное решение ДУ (?) (численно)

[coll3ctor]

Недавно, выполняя численную реализацию тригонометрической интерполяции и программируя метод Эйлера для решения ДУ мне в голову пришла интересная мысль! А именно:
Пусть у нас есть ДУ. Имеются начальные условия. Мы можем построить (нарисовать) множество решений ДУ (интегральные кривые (кстати это не так то просто может оказаться!)). Используя начальные условия, выбираем конкретную интегральную кривую. Интерполируем её (наиболее оптимальным способом) и получаем решение!
Разве не логично?

[svv]

Хочу один момент подчеркнуть.
Вот у Вас есть уравнение $y'=f(x,y)$. Вы берете плоскость $xOy$ и густо-густо строите на ней "поле направлений", вроде такого (левая картинка):

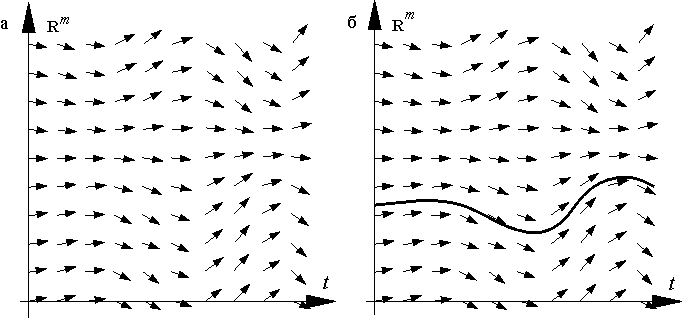
Производная крохотного отрезочка, расположенного в точке $(x, y)$, задается правой частью уравнения $f(x, y)$.
Так вот, решить уравнение -- это значит понять, какие отрезочки принадлежат одной интегральной линии. Т.е. чтобы решить его графически, надо соединить разные отрезочки одной линией (правая картинка). Это тоже нетривиальная операция.
Наверное, всё это Вы и так прекрасно понимали.

[coll3ctor]

svv
да, это я и имел ввиду, под трудностью построения. Преподаватель мой вообще выражался: "угадать кривую в поле направлений".

Ну так, допустим, мы угадали, далее возможно ведь то, как я задумал ?

[svv]

Да, возможно.
Вы ведь не претендуете на то, что Ваше решение точное.

[coll3ctor]

svv в сообщении #527635 писал(а):

Да, возможно.
Вы ведь не претендуете на то, что Ваше решение точное.

Безусловно, нет!

Недавно пытался решить уравнение Рикатти, "вручную" никак не получалось и пришлось решать численно. Вот для таких, я думаю, вполне приемлимо.

Возможно с каким-нибудь методом Рунге-Кутта 4-го порядка при огромном числе итераций этот метод и не сравнится, но он существует ведь! И упирается, получается, в точность определения интегральной кривой ДУ и точности интерполяционного метода.

И, неужели, раньше так никто не делал?

[svv]

Нет, никто.
Хотя для уверенности стоит погуглить "аппроксимация интегральной кривой".

[coll3ctor]

svv

Цитата:

Метод Эйлера является явным, одношаговым методом первого порядка точности, основанном на аппроксимации интегральной кривой кусочно линейной функцией, т. н. ломаной Эйлера.

Эх, вот как :(

Конечно, можно этот метод воплотить в жизнь, но да кому он нужен ?..

PS
Хотелось бы услышать мнения более большего числа форумчан

[bot]

Дык это же метод изоклин, нет? В задачнике Филлипова, помнится, задачи такие есть.

[coll3ctor]

bot в сообщении #527671 писал(а):

Дык это же метод изоклин, нет? В задачнике Филлипова, помнится, задачи такие есть.

метод изоклин - это построение множества интегральных кривых, и только.

[bot]

А Вы что строите? Из этого множества выбираете решение задачи Коши?

[coll3ctor]

bot в сообщении #527677 писал(а):

А Вы что строите? Из этого множества выбираете решение задачи Коши?

ну, вроде бы, да

[Утундрий]

bot в сообщении #527671 писал(а):

это же метод изоклин

Он самый. Полезная, кстати, штука, когда нужно грубо прикинуть фазовый портрет.

[Padawan]

Я не понял при чём тут метод изоклин. Изоклина уравнения $y'=f(x,y)$, это кривая $f(x,y)=C$. Тут же предлагается численное решение аппроксимировать какой-нибудь функцией.

[Утундрий]

Да тут все кони/люди в кучу смешались: изоклины, вариационные методы, пристрелка... Каждый говорит о том, что ему больше нравится

[coll3ctor]

Padawan
Утундрий

вы меня не поняли:) я лишь предложил логичный метод решения ДУ. Просто мне было интересно, делал ли так кто нибудь, возможно ли это, и, самое главное, оптимально ли это.

Метод изоклин лишь один из способов построения интегральных кривых.