Если попытаться решать без теоремы Ко Чао, то можно для начала заметить:
1.

должно быть нечетно, иначе имеем несуществующий пифагоров треугольник
2.

тоже должно быть нечетно, иначе

и если

- четно, то

- нечетно,
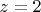
,

- что невозможно
Тогда приходим к необходимости искать решение для

при нечетных

Но даже частные случаи не представляются такими простыми. Например,

имеем

.
Для начала доказательства теоремы Ко Чао можно тоже заметить ряд тривиальных фактов:
если

, то если

четно, то

и

- взаимнопростые, значит

и

, что приводит к

- невозможно.
Пусть

, тогда

,
1. если

- четно, то

и

,
2. если

- нечетно, то

,

.
В нашем случае

,

.
Для первого случая имеем

,

- т.е. это ничего не дает
Для второго случая получаем

- невозможно.
Добавлено спустя 2 часа 10 минут 59 секунд:
В принципе можно продолжить.
Пусть

, тогда

1. если

- четно, аналогично приходим к

2.

- нечетно, тогда

и

Продолжая так по первому случаю всегда будем получать тоже самое. Но мы не можем так делать до бесконечности и рано или поздно придем ко второму случаю.
Тогда для всех порождаемых вторых случаев нужно показать невозможность решения.