2. Стационарная последовательность

имеет спектральную плотность

. Найти спектральную плотность стационарного решения уравнения

.
1. Вот это условие
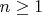
, вообще говоря, делает несколько сомнительным стационарность последовательности.
2. Если бы последовательность

была известна, то стационарное решение уравнения можно было бы найти либо как общее решение записанного разностного уравнения при

, либо просто как частное решение записанного уравнения. Это не ваш случай, так как вам задана
случайная последовательность и её спектральная плотность мощности.
3. Последовательность

получается путём преобразования последовательности

линейной дискретной системой (ЛДС), описываемой разностным уравнением

. Это означает, что спектральную плотность мощности последовательности в стационарном режиме

можно найти путём умножения спектральной плотности мощности последовательности

на квадрат амплитудно-частотной характеристики (АЧХ) системы:

4. АЧХ ЛДС находится как модуль комплексной частотной характеристики (КЧХ) ЛДС. Для определения КЧХ соответствующей ЛДС запишем её разностне уравнение относительно детерминированных сигналов

и рассмотрим преобразование Фурье от его обеих частей:

, откуда для комплексной частотной характеристики системы получим

5. Подробнее можно посмотреть в Основы цифровой обработки сигналов: Курс лекций / Авторы: А.И. Солонина, Д.А. Улахович, С.М. Арбузов, Е.Б. Соловьева, И.И. Гук. - СПб.: БХВ-Петербург, 2003. стр. 211-229.
6. Судя по вашим обозначениям вы должны пользоваться другим учебником. Но суть решения задачи отражена п.3. и заключается в том, что само стационарное решение уравнения вам не потребуется, да и не может быть найдено при случайном воздействии.