В Виленкине "Комбинаторика" есть такой параграф "Жетоны в мешке".
Пусть имеется мешок, в котором

занумерованных жетонов - на них написаны числа

. Из мешка вытаскивают очередной жетон, записывают его номер, затем кладут жетон обратно в мешок. Так получают последовательность из

чисел, каждое из которых заключено в пределах от

до

. Требуется узнать, сколько из получающихся таким образом различных последовательностьей имеют сумму

.
Эту величину обозначим через

.
Существует такая реккурентная формула:
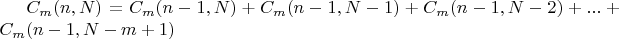
.
В вашем случае нужно найти
 -- Пт ноя 18, 2011 19:26:52 --
-- Пт ноя 18, 2011 19:26:52 --Вашу задачу также можно решить методом включений-исключений. Подумайте как сделать