Замечу, что задача имеет вероятностный смысл, поскольку

- количество нормированных(со старшим коэффициентом 1) неприводимых многочленов степени

над полем
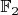
из 2 элементов. Поэтому

- количество нормированных многочленов степени

, являющихся степенью неприводимого, в то время как

- количество всех нормированных многочленов степени

.
По поводу док-ва.
Из определения

легко вывести, что

. Формула обращения Мёбиуса дает

, откуда

.
Edit: На самом деле из определения  видно, что
видно, что  и этого достаточно для дальнейшего.
и этого достаточно для дальнейшего.
Поэтому

На самом деле

, если я нигде не наврал.