Назовите любое число из
![$[-1; 1]$ $[-1; 1]$](https://dxdy-02.korotkov.co.uk/f/d/4/0/d402d4bcde6bf3febbe86ad1662eb01982.png)
— вот вам и предел какой-нибудь подпоследовательности. (Я правильно понял, что значит
частичный предел?)
-- Вс ноя 13, 2011 23:37:24 --lim sin n при n стремящемся в бесконечность,не существует или существует, в чем я и сомневаюсь
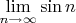
не существует.