1)Для каждого разряда пятизначного числа имеется пять возможностей, значит

2)ну тут как я понимаю формула размещения значит

только вот как факториал высчитывается этого я не помню
3)тут такаой же способ как и в предыдущей задаче,т.е.

но проблема остается такой же
4)ну здесь решение примерно как в первой задаче только 5 и 0 во всех случаях должна быть на последнем месте (что ограничивает количество ответов и число 0 не может быть на первом месте) следовательно

5)ну думаю что всего 33 буквы каждая разбить по 5на каждый символ,получается обратное действие только вот как его записать тоже не особо представляю
Не знаете, что такое факториал?)
Всё очень просто, факториал от некого натурального числа - есть произведение всех натуральных чисел от единицы до этого числа. Тоесть:

. Например

1) Вы не учли, что цифры не должны повторятся. Поэтому для первой цифры - 5 возможностей, для второй - уже 4, для третий 3... итого
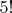
Дальше не смотрел.