aquatko писал(а):
Понятия не имею, как искать
 без
без условия, что функция

...
Очевидно описка: имелось в виду как искать

?
1. Проблемы с нулем в правой части

вообще нет: перенесите в

все в одну сторону

.
Хотя, честно говоря, в этом действиии и нет особой необходимости.
2. В случае двух переменных для

Ваша формула верная, а для
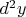
- нет.
3. Вопрос, аналогичный Вашему для 3-х переменных уже обсуждался
http://dxdy.ru/topic13035.html.
3.

читается по-русски как латех. Название

- греческого происхождения, сравните русское "техника".