Асимптотика

[Sonic86]

Введем класс $\mathcal{L}$ логарифмически-экпоненциальных функций Харди (упомянуто в Конкретной математике в начале главы Асимптотика).
1. $f(n) =A \in \mathcal{L}$.
2. $f(n) =n \in \mathcal{L}$.
3. $f(n), g(n) \in \mathcal{L} \Rightarrow f(n) \pm g(n) \in \mathcal{L}$.
3. $f(n) \in \mathcal{L} \Rightarrow \ln f(n) , \exp(f(n)) \in \mathcal{L}$.
В этом классе для любой пары функций $f,g$ верно $f \prec g$ или $f \succ g$, либо $f \sim C g$ (всегда существует $\lim \frac{f}{g} \in \mathbb{R} \cup \{ \infty \}$, здесь $f \prec g \Leftrightarrow \frac{f}{g} = 0$, $f \succ g \Leftrightarrow \frac{f}{g} = \infty$). Т.е. все функци образуют иерархию.
От себя замечу, на нестрогом языке, который надо будет исправить, что иерархия по операции $\cdot$ неархимедова, т.е. для некоторой $f(n)$ всегда $f(n) \cdot ... \cdot f(n) \prec \exp (f(n))$ + иерархия неполна. Полнота была бы очень удобна при формулировке теоремы о сходимости знакоположительного ряда (интеграла) $\sum f(n)$ для $f(n) \in \mathcal{L}$ (имеется ввиду, что $\frac{1}{n}, \frac{1}{n \ln n}, \frac{1}{n \ln n \ln \ln n}, ... \to y^*(n)$, тогда знакоположительный ряд $\sum f(n)$ для $f(n) \in \mathcal{L}$ сходится $\Leftrightarrow f(n) \prec y^*(n)$).

Рассмотрим в $\mathcal{L}$ последовательность функций $\exp _k(n)$ для $k \in \mathbb{N}$: $\exp _0(n) = n, \exp _{k+1}(n)=\exp (\exp _k(n)), \exp _{k-1}(n)=\ln (\exp _k(n))$. Проще говоря, $..., \ln \ln n, \ln n , n , \exp (n), \exp \exp (n), ...$.
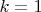
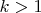
Если рассмотреть приращение $D: Dy=y(n+1)-y(n)$ и производную этих функций, то окажется, что $D( \exp _k(n)) \sim (\exp _k(n))'$ для $k \leq 0$, для $k=1$ они отличаются на константу: $1$ и $e-1$ соответственно, а при $k>1$ первая асимптотически быстрее второй.
Предположим, что $m(y)=\frac{Dy}{y'}$ - неубывающая функция при $y$ пробегающем $\mathcal{L}$ в порядке возрастания (мне это очевидно, но доказательства нет). Уже на примере наших функций видим, что сначала $m(y)=1$ а потом возрастает "до бесконечности".

Задача: найти $f \in \mathcal{L} : m(f)=1$ и $f$ - последняя функция по иерархии, на которой $m(f)$ принимает значение 1 (т.е. если $g \succ f$, то $m(g)>1$) (значения $m(y)$ - функции).

З.Ы. Если существует соответствующий раздел матанализа - отошлите меня к книжкам. Если раздела явно нет, и кто-то будет решать задачу, просьба указать нормальные обозначения и уровень обобщения, поскольку я сам точно правильно не написал.

[Xaositect]

Лично я нигде ничего похожего не видел.

Итак. У нас есть некое множество функций $\mathcal{L}$ и функционал $m\colon\mathcal{L}\to \mathcal{L}$. Вы утверждаете, что он монотонный, я подозреваю, что в следующем смысле: $f\preceq g\Rightarrow m[f] \leq m[g]$ для достаточно больших значений аргумента. Верно?
Естественно, что сравнивать $m$ с $1$ мы можем только асимптотически, т.к. у нас могут быть ф-и $f\sim g$ такие, что $m[f]\neq m[g]$ (но $m[f]\sim m[g]$). Так что последний вопрос надо, по всей видимости, переформулировать так: существует ли максимальная (относительно $\preceq$) функция, для которой $m[f]\sim 1$ и если существует, то какая это функция.
Ладно, подумаем. Надо сначала монотонность $m$ доказать.

[Sonic86]

Xaositect в сообщении #462881 писал(а):

Итак. У нас есть некое множество функций $\mathcal{L}$ и функционал $m\colon\mathcal{L}\to \mathcal{L}$. Вы утверждаете, что он монотонный, я подозреваю, что в следующем смысле: $f\preceq g\Rightarrow m[f] \leq m[g]$ для достаточно больших значений аргумента. Верно?

Да, только $m[f]$ - тоже функция, так что, наверное, можно просто $f \preceq g\Rightarrow m[f] \preceq m[g]$

Xaositect в сообщении #462881 писал(а):

Так что последний вопрос надо, по всей видимости, переформулировать так: существует ли максимальная (относительно $\preceq$) функция, для которой $m[f]\sim 1$ и если существует, то какая это функция.

Ну да.

[Xaositect]

Sonic86 в сообщении #462886 писал(а):

Xaositect в сообщении #462881 писал(а):

Итак. У нас есть некое множество функций $\mathcal{L}$ и функционал $m\colon\mathcal{L}\to \mathcal{L}$. Вы утверждаете, что он монотонный, я подозреваю, что в следующем смысле: $f\preceq g\Rightarrow m[f] \leq m[g]$ для достаточно больших значений аргумента. Верно?

Да, только $m[f]$ - тоже функция, так что, наверное, можно просто $f \preceq g\Rightarrow m[f] \preceq m[g]$

Верно, но судя по тому, что Вам нужно различать случаи $m[f]\sim m[g]$ и $m[f]\sim C m[g]$, в правой части нужно более тонкое неравенство.

[Xaositect]

Так, похоже я в этом разобрался.
Ограничимся только бесконечно возрастающими функциями $\mathcal{L}_{\infty} = \{f\in\mathcal{L}|f\succ 1\}$. Не уверен, что для ограниченных для бесконечности наш функционал вообще монотонен.
Наши функции аналитичны при достаточно больших значениях аргумента. Запишем формулу Тейлора:
$\frac{\Delta f}{f'} = 1 + \frac{f''}{2f'} + \frac{f'''}{6f'} + \dots + \frac{f^{(n)}(x + \xi)}{n! f'}$, $0< \xi < 1$
Вспомогатеьное утверждение: $\frac{f}{g}\to c \Leftrightarrow \frac{f'}{g'}\to c$. Доказывается с помощью теоремы Коши, с учетом бесконченой великости наших функций: $f \sim f - f(a)$.
Возможны следующие случаи:
$f''\succ f' \Rightarrow \frac{\Delta f}{f'}\to \infty$
$\frac{f''}{f'}\to c \Rightarrow \frac{f^{(n+1)}}{f'}\to c^n$. Надо исследовать сходимость остаточного члена. и получить, что $\frac{\Delta f}{f'}\to \frac{e^c - 1}{c}$. Вот в исследовании сходимости я мог ошибиться, но как-то все уж слишком красиво выходит, мне кажется, это правда.
Итак, $\frac{\Delta f}{f'} \to 1 \Leftrightarrow \frac{f''}{f'}\to 0$
Кстати, $\frac{f''}{f'} = (\ln f')'$

Насколько я понимаю, отсюда следует, что максимума и даже точной грани у искомого множества не существует, но критерий достаточно простой.

[Sonic86]

О! Классно! Спасибо большое!

Цитата:

Итак, $\frac{\Delta f}{f'} \to 1 \Leftrightarrow \frac{f''}{f'}\to 0$
Кстати, $\frac{f''}{f'} = (\ln f')'$

Кажется $(\ln f')' \to 0 \Leftrightarrow \ln f' \prec x$.
Доказывается, кажется так.

Цитата:

$\frac{f}{g}\to c \Leftrightarrow \frac{f'}{g'}\to c$

Значит, подставляя $c=0$ и интегрируя обе части, получим то, что нужно.
(кстати, что за теорема Коши?)
Вспомогательное утверждение можно переписать как
$\frac{f}{g} \sim \frac{f'}{g'}$
И должно быть
$\frac{f}{g} \sim \frac{\Delta f}{\Delta g}$ (теорема Штольца)
Еще кое-что вспомнил:
$f \prec g \Rightarrow (fg)' \sim f \cdot g'$ (аналогично с разностями)
$f \prec g \Rightarrow \int fg dx \sim f \int gdx dx$ (аналогично с суммами)
Еще:
$f \sim g \Rightarrow \int fdx - \int gdx \preceq \frac{\int fdx}{x}$.

Для более узкого класса функций вида $f \sim x^{a_0} \ln _1^{a_1} x ... \ln _s^{a_s} x$
будет $\int fdx \sim C_f \cdot f \cdot \prod\limits_{j=0}^k \ln _j x$, где $k: a_0=...=a_{k-1}=-1, a_k \neq -1$ (для суммирования аналогично). Интересно было бы знать, как асимптотика в общем виде находится.

Еще задачка: найти все $f \in \mathcal{L}: \lim\limits_{x \to + \infty} \frac{\int fdx}{xf} = + \infty$.

[Xaositect]

Sonic86 в сообщении #463496 писал(а):

(кстати, что за теорема Коши?)

$f, g$ дифференцируемы на $[a,b]$, $g'$ не обращается в 0 => $\frac{f(b) - f(a)}{g(b) - g(a)} = \frac{f'(\xi)}{g'(\xi)}$