метод Лагранжа, найти канонический вид квадратичной формы

[GanGSISoft]

Задание: При помощи метода Лагранжа найдите канонический вид и одно из невырожденных линейных преобразований переменных, приво-
дящих квадратичную форму
$x^2+5y^2-z^2+6xy+4xz$
Я почитал это: topic34031.html читал другое, но никак не въеду с чего начинать.
Как я понял, нужно как то отобрать иксы, и перегнать их в полный квадрат с y и z
Потом тоже проделать с игриками
И останется одни Z
Получается a=(x+y+z) b=(y+z) c=(z) где перед x,y,z могут стоять разные коэфициенты.
Но как это получить, и как найти "одно из невырожденных линейных преобразований переменных" не пойму никак.
Помогите пожалуйста.

[Slava M]

Начните выделять полные квадраты. После выделения проведите замену переменных. Замена переменных и будет линейным преобразованием так нужным Вам. Выпишите что у Вас получается?

Советую прочесть http://nature.web.ru/db/msg.html?mid=1151602&uri=ch1node5.html. А еще лучше прочесть Вам и предыдущий параграф.

[mihailm]

(Оффтоп)

На конкурс)

[GanGSISoft]

Я уж извиняюсь за то что я такой идиот, но не пойму как выделить первый квадрат. Надо получить я так понимаю $(x+y+z)^2$?
Я что-то сделал, но иксы все не пропали.
$x^2+5y^2-z^2+6xy+4xz=x^2+y^2+z^2+2xy+2xz+2yz-2z^2+4y^2+4xy+2xz-2yz=(x+y+z)^2-2z^2+4y^2+4xy+2xz-2yz$

[Sonic86]

Дык квадрат надо выделять так, чтобы все иксы исчезли. Зачем Вы взяли $(x+y+z)^2$? Можно же $(ax+by+cz)^2$, причем $a,b,c$ берете как душе угодно.
Если затрудняетесь, попробуйте выделите квадрат из выражения $x^2+2a_1x+...+2a_nx$.

[Slava M]

Попробуйте сначала выделить $(x+3y+2z)^2$.

[Sonic86]

(Оффтоп)

Slava M писал(а):

Попробуйте сначала выделить $(x+3y+2z)^2$.

эх, ну должен же человек сам думать...

[GanGSISoft]

Спасибо вам. Я толь сейчас понял как нужно было выделять полный квадрат, стыдно мне, а ещё в университете учусь.
Вот только получу я $(x^2+y^2+z^2)+(y^2+z^2)+(z^2)$, как их этого получить кононический вид и одно из невырожденных линейных преобразований переменных?

[Sonic86]

GanGSISoft писал(а):

Вот только получу я $(x^2+y^2+z^2)+(y^2+z^2)+(z^2)$, как их этого получить кононический вид и одно из невырожденных линейных преобразований переменных?

канонический.
Чего-то я не понял, что Вы хотите.
Вы хотите получить представление данной квадратичной формы вида $(x^2+y^2+z^2)+(y^2+z^2)+(z^2)$? А зачем? Вам надо выделить квадраты, а потом делать линейные замены вида $x_j' = \text{выражение под }j\text{-м квадратом}$.

[GanGSISoft]

Цитата:

А зачем?

Мне по условию задачи это нужно найти.
Но в общем то ясно с каноническим видом, но "одно из невырожденных линейных преобразований переменных", что это такое?

[Slava M]

Вы не слушаете что Вам говорят, скажем Sonic86.

Давайте делать всё по очереди. Запишите квадратичную форму предварительно выделив квадраты по очереди начиная с указанного Вам первого.

[Sonic86]

(Оффтоп)

Slava M писал(а):

Вы не слушаете что Вам говорят, скажем Sonic86.

Это почему???

GanGSISoft писал(а):

Цитата:

А зачем?

Мне по условию задачи это нужно найти.

Это неверно. Вам надо привести форму к виду $x_1^2 \pm ... \pm x_s^2$ для некоторого $s \leq \text{размерности задачи}$. Выражение $(x^2+y^2+z^2)+(y^2+z^2)+(z^2)$ к таковым не относится. Вы выделите квадраты уже до конца.

GanGSISoft писал(а):

"одно из невырожденных линейных преобразований переменных", что это такое?

Линейное преобразование - это преобразование вида $X'=AX$, где $X$ - вектор размерности $n$, а $A$ - матрица. Преобразование невырожденно, если $\det A \neq 0$.
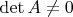
Я же Вам говорил:

Sonic86 писал(а):

Вам надо выделить квадраты, а потом делать линейные замены вида $x_j' = \text{выражение под }j\text{-м квадратом}$.

это и будет линейное преобразование. Для него легко доказать, что оно невырожденное (матрица будет иметь треугольный вид).