Неопределённые интегралы

[spaits]

Play в сообщении #432289 писал(а):

Собственно я не силён в матане, но задание надо сдать. Помогите пожалуйста разобраться. Мне бы начать..а дальше я сам решу. Помогите пожалуйста. Заранее благодарен.

Знак интеграла не нашёл как ставить...

1. $\int \frac {x^2}{1-x^4}dx$

2. $\int \frac {x^5}{(x-1)^2 (x^2-1)}dx$

3. $\int \frac {x^3 -2x+4}{x^3 (x-2)^2}dx$

4. $\int \frac{x^3 -6}{x^4 +6x^2 +8}dx$

5. $\int \frac {\sqrt {x^3}- \sqrt[3]{x}}{6\sqrt[4]{x}}dx$

6. $\int e^x sin4xdx$


Напишите пожалуйста как решать каждый интеграл и если не сложно то написать как именно. Повторюсь, что решение всё мне не обязательно.

Пример 5.
Перейдите к степеням с дробным показателем, разделите числитель на знаменатель, получите разность степенных функций. От степенной функции интеграл брать умеете? Да, $\frac16$ можно вынести за знак интеграла (можно и не выносить).
$\int\frac{\sqrt{x^3}- \sqrt[3]{x}}{6\sqrt[4]{x}}dx=\frac{1}{6}\int{(x^{\frac54}-x^{\frac{1}{12}}) dx=$ ...
Дальше решайте сами. Надеюсь, поняли, что $\frac32-\frac14=\frac54$; $\frac13-\frac14=\frac{1}{12}$.

-- Пт апр 08, 2011 20:49:17 --

Дальше Вы к $\frac54$ прибавляете $1$ (по формуле степенного интеграла): $\frac54+1=\frac94$; также получаете показатель степени при интегрировании второй степени $\frac{1}{12}+1=\frac{13}{12}$.
Повторите формулу степенного интеграла! Напишите ее здесь.

[Play]

Простите что пропадал - болел.

Я по-порядку решил решать. Интеграл под номером 2 не смог решить, интеграл 3 решил и вот собственно решение:

$\int \frac{x^3-2x+4}{x^3 (x-2)^2} = \frac {A}{x^3} +\frac {B}{x^2} + \frac {C}{x} + \frac {D}{(x-2)^2}+\frac {E}{x-2}=.... ;$

$x^3-2x+4 = Ax^6-6x^2+12Ax^4-8Ax^3 +Bx^7-6Bx^3+12Bx^5-8Bx^4+Cx^8-6Cx^4+12Cx^6-8Cx^5+Dx^7-2Dx^6+Ex^8-4Ex^7+4Ex^6;$

$x^8(C+E)+x^7(B+D-4E)+x^6(A+12C-2D+4E)+x^5(12B-8C)+x^4(12A-8B-6C)+x^3(-8A-6B)+x^2(-6A);$

$(1)0=C+E$
$(2)0=B+D-4E$
$(3)0=A+12C-2D+4E$
$(4)0=12B-8C=3B-2C$
$(5)0=12A-8B-6C=6A-4B-3C$
$(6)1=-8A-6B=> -1=8A+6B $
$(7)0=-6A$

$(7) => A=0$
$(1) => C=-E$
$(6) => 6B=-1 => B= -\frac {1}{6}$
$(5) => -4*(-\frac{1}{6}) -3C=0 => C=\frac{2}{9}$
$(1) => E= -\frac{2}{9}$
$(3) => 12*\frac{2}{9}-2D+4*(-\frac{2}{9})=0 => D=\frac{8}{9}$

$-\frac{1}{6}\int\frac{1}{x^2}dx+\frac{2}{9}\int\frac{dx}{x}+\frac{8}{9}\int\frac{1}{(x-2)^2}dx-\frac{2}{9}\int{dx}{x-2}$

Отдельно: $\int\frac{dx}{(x-2)^2} <t=x-2; dx=dt> = \int\frac{dt}{t^2}=\frac{t^3}{3}=\frac{(x-2)^3}{3}$

Продолжение:

$-\frac{x^3}{18}+\frac{2}{9}\ln|x|+\frac{8(x-2)^3}{27}-\frac{2}{9}\ln|x-2|$

Могут быть опечатки

-- Вт апр 12, 2011 22:11:01 --

Цитата:

Повторите формулу степенного интеграла! Напишите ее здесь.

$\int x^ndx+C=\frac{x^{n+1}}{n+1}$
Получается:
$\frac{4x^{\frac{9}{4}}}{54}-\frac{12x^{\frac{13}{12}}}{13}$
Я разбил интеграл суммы на сумму интегралов и применил эту формулу, а также умножил первую дробь на $\frac{1}{6}$.

[laplas_the_best]

Ошибки есть, тут

$(3)$ $1=...$
$(1)$ $-2=..$
$(0)$ $4=...$

А до этого вы не очень подробно написали -- как приводили к общему знаменателю, поэтому -- тяжело проверять=)

-- Вт апр 12, 2011 21:29:02 --

Play в сообщении #434167 писал(а):

$ \int\frac{dt}{t^2}=\frac{t^3}{3}$

А это -- неверно, тк $\int\frac{dt}{t^2} \ne \int t^2dt$

P.S. Лучше приписывать $+const$ при подсчете неопределенных интегралов.

[Play]

Цитата:

Ошибки есть, тут

Поясните пожалуйста.
К общему знаменателю так приводил:

$\frac{Ax^2x(x-2)^2(x-2)+Bx^3x(x-2)^2(x-2)+Cx^3x^2(x-2)^2(x-2)+Dx^3x^2x(x-2)+Ex^3x^2x(x-2)^2}{x^3x^2x(x-2)^2(x-2)}= \frac {Ax^3(x^3-6x^2-4x-8)+Bx^4(x^3-6x^2+12x-8)+Cx^5(x^3-6x^2+12x+4x-8)+Dx^7-2Dx^6+Ex^8-4Ex^7+4Ex^6}{x^6(x-2)^3}$

я правда не знаю нужно ли так делать знаменатель? Мы обычно сразу числитель расписывали.

-- Вт апр 12, 2011 22:44:53 --

Цитата:

А это -- неверно

Точно, сглупил, самому стыдно.
Так получается $\int \frac{dt}{t^2} = \int t^{-2}dt=\frac {t^{-1}}{-1} = -\frac{1}{t} = -\frac{1}{x-2}$

[spaits]

laplas_the_best в сообщении #434180 писал(а):

Интеграл под номером 2 не смог решить,

В числителе пятая степень, в знаменателе - четвертая степень многочлена. Надо выделить целую часть, потому что в виде суммы элементарных дробей можно представить лишь правильную дробь (у которой степень многочлена в числителе меньше, чем в знаменателе). Разделите с остатком числитель на знаменатель.
Это первое. А потом уже знакомый Вам интеграл от правильной дроби. Однако, желательно перед этой процедурой убрать из числителя еще и производную знаменателя. В Вашем примере степень многочлена в числителе уменьшится на единицу. А бывает - сразу интеграл берется.
Если Вы не умеете делить многочлен на многочлен, то скажите - Вам помогут.

[laplas_the_best]

Цитата:

$$\frac{x^3-2x+4}{x^3 (x-2)^2} = \frac {A}{x^3} +\frac {B}{x^2} + \frac {C}{x} + \frac {D}{(x-2)^2}+\frac {E}{x-2}=$$

$$=\frac{Ax^2x(x-2)^2(x-2)+Bx^3x(x-2)^2(x-2)+Cx^3x^2(x-2)^2(x-2)+Dx^3x^2x(x-2)+Ex^3x^2x(x-2)^2}{x^3x^2x(x-2)^2(x-2)}= $$

Дело в том, что общий знаменатель $x^3(x-2)^2$ (хорош сам факт, что вы показали, что выбрали не самый оптимальный знаменатель, тк дальше нельзя приравнивать числители, так как знаменатели различны).
А вот следующей строчкой (после того, как тут исправлено) можно писать без знаменателя, так как знаменатели слева и справа -- равны (а у вас они на данном этапе не равны).

[Play]

Так я не понял? где ошибка то сама? я ведь только знаменатель не правильно написал. А числитель то то же что и у меня. Я так понял вы уже исправленную мне показали. Или просто процитировали?

Цитата:

Если Вы не умеете делить многочлен на многочлен, то скажите - Вам помогут.

Знаю что выглядит нагло, но я ничего не умею в этом плане..а точнее не понимаю с ваших слов. Мне было бы легче, если вы вспомнили мою самую первую просьбу - помочь начать. Так как для меня это и является главной трудностью. Так же я не требую халявы, но у меня просто сейчас сложное время, а все эти интегралы нужно сдать в понедельник, помимо других предметов. Поймите пожалуйста.

[spaits]

laplas_the_best в сообщении #434294 писал(а):

Цитата:

$$\frac{x^3-2x+4}{x^3 (x-2)^2} = \frac {A}{x^3} +\frac {B}{x^2} + \frac {C}{x} + \frac {D}{(x-2)^2}+\frac {E}{x-2}=$$

$$=\frac{Ax^2x(x-2)^2(x-2)+Bx^3x(x-2)^2(x-2)+Cx^3x^2(x-2)^2(x-2)+Dx^3x^2x(x-2)+Ex^3x^2x(x-2)^2}{x^3x^2x(x-2)^2(x-2)}= $$

Дело в том, что общий знаменатель $x^3(x-2)^2$ (хорош сам факт, что вы показали, что выбрали не самый оптимальный знаменатель, тк дальше нельзя приравнивать числители, так как знаменатели различны).
А вот следующей строчкой (после того, как тут исправлено) можно писать без знаменателя, так как знаменатели слева и справа -- равны (а у вас они на данном этапе не равны).

Я смотрю, Вы здесь развлекаетесь.
Числители дробей можно приравнять, если знаменатели одинаковые. Вам пояснили. Начались шутки. Конечно, шутки хорошо.
Также я пояснила, с чего начать решение примера 2, а именно, с деления многочлена на многочлен.
А потом - знакомый Вам интеграл.
Я не буду Вам пояснять ничего до тех пор, пока не пойму, чего Вы хотите. А пока понять трудно.

[Play]

$\frac{A(x-2)^2+Dx^3}{x^3(x-2)^2}+\frac{Bx(x-2)+Cx^2(x-2)+Ex^3}{x^3(x-2)}=\frac{A(x-2)^2+Dx^3+Bx(x-2)^2+Cx^2(x-2)^2+Ex^3(x-2)}{x^3(x-2)^2}$

Да, мне делать нечего как развлекаться тут. Кроме этого решения, другого не нашёл. Называйте меня как хотите, если это вам жизнь лучше сделает.

[Алексей К.]

Правильно. Только предпоследнее равенство, сумма двух дробей, — немного лишняя работёнка.
Теперь числитель надо расписывать в виде $(C+E)x^4+(\ldots)x^3+\ldots$.
Я сосчитал только один (лёгкий) коэффициент. И теперь этот числитель можно будет сравнить и исходным числителем.
Сразу видим $C+E=0$, то есть $E=-C$. Ну и с остальными возиться аналогично.

[spaits]

Play в сообщении #434458 писал(а):

$\frac{A(x-2)^2+Dx^3}{x^3(x-2)^2}+\frac{Bx(x-2)+Cx^2(x-2)+Ex^3}{x^3(x-2)}=\frac{A(x-2)^2+Dx^3+Bx(x-2)^2+Cx^2(x-2)^2+Ex^3(x-2)}{x^3(x-2)^2}$

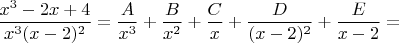
Да, мне делать нечего как развлекаться тут. Кроме этого решения, другого не нашёл. Называйте меня как хотите, если это вам жизнь лучше сделает.

Приравниваем числители.
$x^3-2x+4=A(x-2)^2+Dx^3+Bx(x-2)^2+Cx^2(x-2)^2+Ex^3(x-2)$.
Если сразу раскрыть скобки и приравнять коэффициенты при одинаковых степенях $x$, то линейная система уравнений получается сложной. Можно применить комбинированный метод: два коэффициента найти другим способом, а именно, даем иксу значения, при которых большая часть скобок в правой части равна нулю.
$x=2; 8=8D; D=1$;
$x=0; 4=4A; A=1$.
Теперь эти значения $A$ и $D$ подставляем в уравнение и находим остальные три коэффициента.
$x^3-2x+4=(x-2)^2+x^3+Bx(x-2)^2+Cx^2(x-2)^2+Ex^3(x-2)$.
Слагаемые с известными коэффициентами переносим в левую часть:
$-x^2+2x=Bx(x^2-4x+4)+Cx^2(x^2-4x+4)+Ex^3(x-2)$;
$-x^2+2x=(C+E)x^4+(B-4C-2E)x^3+(-4B+4C)x^2+4Bx$.
Приравниваем коэффициенты при одинаковых степенях.
Из уравения $4B=2$ сразу находим: $B=\frac12$.
Далее: $-4B+4C=-1$; $-2+4C=-1$; $C=\frac14$.
$C+E=0$; $E=-C=-\frac14$.
Уравнений больше, чем неизвестных, они не противоречивы, проверьте, выполняется и уравнение $B-4C-2E=0$.
Подставляем полученные значения коэффициентов в Ваше разложение подынтегрального выражения на элементарные дроби и берем элементарные интегралы.
Выписываю отдельно найденные значения коэффициентов: $A=1$; $D=1$; $B=\frac12$; $C=\frac14$; $E=-\frac14$.