представление числа n! в виде суммы его n различных делителе

[Xenia1996]

При каких натуральных $n$ число $n!$ представимо в виде суммы его $n$ попарно различных натуральных делителей?

(Попытка)

Я попыталась доказать по индукции, что для любого $n\ge 3$ условие задачи выполняется.

При $n=3$ имеем $1+2+3=6$
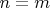
Предположим, что утверждение верно для $n=m$, то бишь, $m!$ представимо суммой m его делителей.
Умножим каждый из m делителей, являющихся слагаемыми в этой сумме, на m+1 и получим в сумме $(m+1)!$
Теперь представим наименьший из делителей в виде суммы двух слагаемых: 1 и m.
Поскольку $(m+1)!$ делится на m, имеем число $(m+1)!$ в виде суммы m+1 попарно различных его делителей.

Где ошибка в этом рассуждении?

[Someone]

Вы не оговорили, что среди тех делителей, сумма которых есть $m!$, имеется число 1. Поэтому после умножения на $m+1$ наименьший делитель может оказаться больше $m+1$, и его нельзя будет представить как сумму $m$ и $1$.