Рассмотрим сначала однородную задачу (

). Пусть

, тогда

- аналитическая на всей комплексной плоскости с разрезом
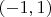
, исчезает на бесконечности и на разрезе удовлетворяет условию

(формула Сохоцкого-Племеля). Отсюда следует, что

(в отличие от случая разреза вдоль всей прямой, когда

может быть, в известном смысле, произвольной), стало быть, опять-таки по формуле С.-П.

.
Вернемся к неоднородной задаче. Представим правую часть в виде

(решение задачи о скачке), где

, тогда исходное уравнение перепишется в виде

, где

. Таким образом, задача сводится к тому, чтобы аналитически продолжить функцию

, принадлежащую введенному выше классу функций, через разрез.
Функций, допускающих такое продолжение, бесконечно много, например,

,

; искомое продолжение функции задается умножением на

на разрезе. Заметим, что при действительных

оператор умножения будет унитарным. Таким образом, мы определили линейный функционал на подмножестве функций (ограниченный при действительных

). Осталось выбрать всюду плотное подмножество (например, указанные функции при действительных

) и продолжить функционал на все пространство.