Однако это сильно сказано. В таком случае, пожалуйста, приведите контрпримеры.
Да, что-то это я погорячилась :) Обычная формула последовательного усреднения :)
В оправдание себя - исправьте формулу в сообщении
post410985.html#p410985, иначе
![$\mathsf E[\xi\mathcal G]$ $\mathsf E[\xi\mathcal G]$](https://dxdy-03.korotkov.co.uk/f/a/c/1/ac1eb5cce1d9d3ff6fa52b3d97f0c26a82.png)
воспринимается только как матожидание по событию из
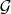
, а равенство - как тождество на всех событиях. Именно так я его и прочла.