Есть такая теоремка небанальная ( Lindenstrauss Tzafriri Classical Banach Spaces I): В сепарабельном банаховом пространстве

существуют фундаментальная система векторов
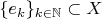
и тотальная система векторов

такие, что

.
Отсюда сразу следует, что

искомый компактный инъективный оператор.
-- Sun Jan 09, 2011 15:49:38 --mathoverflow поинтересоваться..
там одни идиоты пасутся: я и их спросил про изоморфность
![$C^1[0,1]$ $C^1[0,1]$](https://dxdy-01.korotkov.co.uk/f/4/c/9/4c9191dbd496aa445a139d7b0ecfb19e82.png)
и
![$C[0,1]$ $C[0,1]$](https://dxdy-01.korotkov.co.uk/f/c/a/1/ca1e69cd98bea147d53c53dda6988e1882.png)
, а они начали мне хором говорить, что это homework exercise. Больше всего мне подсказка их понравилась :
![$C^1[0,1]/\mathbb{R}\sim C[0,1]$ $C^1[0,1]/\mathbb{R}\sim C[0,1]$](https://dxdy-03.korotkov.co.uk/f/2/c/b/2cb713203af40569b0ae44eea1cb24ff82.png)
. Очевилно, это наблюдение вершина их способностей.
