Сумма ряда (численное решение для комбинаторной задачи)

[mihiv]

yuriyyy10 в сообщении #369168 писал(а):

Определить количество вариантов $N$ построения стопы (стопа - куча, ряд предметов, наложенных один на другой – С.И. Ожегов, Словарь русского языка) высоты $h$ с помощью пластин, толщины которых равны: $e$ и $w$... примем длину самой тонкой пластины толщины $e$ за единицу длины; если в стопе имеется $k$ пластин толщины $w$, то они занимают часть высоты $h$, равную $k w$, и поэтому высота, занимаемая пластинами толщины $e$ будет равна

$$h-k w;$$

общее количество пластин, с учетом того, что толщина тонких пластин принята за единицу длины

Вы все же определитесь с тем,что такое $e$- длина или толщина.По смыслу задачи конечно же толщина.Второй момент:величины $h$ и $w$ входят в комбинаторные формулы,поэтому это целые безразмерные числа.Мне кажется правильнее была бы такая запись:высота стопы $H=he$,толщина пластины $W=we$,тогда $\frac h{w^2}$ ,естественно, безразмерная величина и условие $\frac h{w^2}\leqslant 1$,может быть переписано в виде:$\frac HW\leqslant \frac We$,имеющем понятный "физический смысл".

[yuriyyy10]

Была недоработка изложения. В результате тянулся "хвост" физического смысла.
Вот сами значения:
$h=3*10^{20}$; $w=2*10^{8}$; $e=1$.
Отсюда:
$\frac h{w^2}={0,75 *{10^{4}}>>1$.

[Ales]

Производящая функция: $\frac 1{1-x-x^{\frac w e}}$.
Разложить ее в ряд Тейлора в нуле. Коэффициент при степени $\frac h e$ будет искомым числом.

[Хорхе]

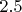
Ну вот я об этом и писал. Но тут действительно нужна хорошая асимптотика для корня $x_k$ уравнения $1-x-x^{k}$ при больших $k$. Ну ладно бы просто асимптотика, нам нужно $x_k^{k^{a}}$, где $a$, судя по числам, которые дает yuriyyy10, в районе $2.5$. Я разве что для $x_k^k$ могу что-то вразумительное написать.

-- Чт ноя 04, 2010 18:11:28 --

Проблема в том, что остаточные члены в асимптотике для $x_k$ плохо себя ведут. Если я не ошибаюсь, где-то так:

$$ x_k = 1-\frac{\ln k}{k} + \frac{\ln\ln k}{k} -\frac{\ln \ln k}{k \ln k} + \dots, $$

отсюда получается бесплатно и асимптотика для $x_k^k$. Но, понятно, что дальше возводить такую асимптотику в степень $k$ безнадежно, уж слишком слабо она убывает. Но нам нужна десятипроцентная точность, и в таком случае это что-то совершенно безнадежное. Я пытался угадать асимптотику $x_k^{k^a}$, но не сильно преуспел. Что еще можно делать, не знаю. Методом перевала тоже не вышло, правда, у меня с ним не очень.

(Видимо, это все не проще, чем работать с суммами биномиальных коэффициентов.)

-- Чт ноя 04, 2010 18:23:12 --

Короче говоря, я уже сдался :( Мне кажется, что тут есть некий ad hoc метод, которого я не знаю.

RIP, ау!

[Ales]

Или если использовать кратность $h$ и $w$ такая функция $\frac{(1-x)^{k-1}}{(1-x)^k-x}$.
Где $k=\frac w e$.
Искать коэффициент ряда Тейлора при степени $\frac h w$.

[Хорхе]

Ales в сообщении #370089 писал(а):

Или если использовать кратность $h$ и $w$ такая функция $\frac{(1-x)^{k-1}}{(1-x)^k-x}$.

Не понял, откуда это.

[Ales]

Хорхе в сообщении #370124 писал(а):

Ales в сообщении #370089 писал(а):

Или если использовать кратность $h$ и $w$ такая функция $\frac{(1-x)^{k-1}}{(1-x)^k-x}$.

Не понял, откуда это.

$\frac 1 {1-x-x^k} = \frac 1 {(1-x^k)(1-\frac x{1-x^k}) }$
Если выкинуть все члены ряда Тейлора не кратные $x^k$ получим:
$\frac 1 {(1-x^k)(1-\frac {x^k}{(1-x^k)^k}) }$.
Заменим $x^k$ на $x$, получается $\frac{(1-x)^{k-1}}{(1-x)^k-x}$.

Но не знаю: полезно ли это.

[Хорхе]

Полезно безусловно, а вот правильно ли?
------------------------------------------
Кажись, понял. Ловко! Подумаю завтра.

[Ales]

yuriyyy10 в сообщении #369909 писал(а):

Была недоработка изложения. В результате тянулся "хвост" физического смысла.
Вот сами значения:
$h=3*10^{20}$; $w=2*10^{8}$; $e=1$.
Отсюда:
$\frac h{w^2}={0,75 *{10^{4}}>>1$.

$nk=3*10^{20}$
$k=2*10^8$

Пользуемся производящей функцией: $\frac 1{1-x-x^k}$.
Ответ - коэффициент при члене $nk$-ой степени ряда Тейлора этой функции в нуле.
Благодаря кратности $nk$ и того, что $n>>k$, хорошее относительное приближение для ответа:
$\frac 1 {(1-x)^n (k(1-x)+x)}$, где $x$ - вещественный корень уравнения $1-x-x^k=0$.

[Хорхе]

Ales в сообщении #370803 писал(а):

Благодаря кратности $nk$ и того, что $n>>k$, хорошее относительное приближение для ответа:
$\frac 1 {(1-x)^n (k(1-x)+x)}$, где $x$ - вещественный корень уравнения $1-x-x^k=0$.

Это все распрекрасно, только вот непрактично. Я выше писал про асимптотику этого корня, она безнадежная.

[Ales]

Корень находим методом Ньютона:
$x_0=1$
$x_{j+1}=x_j-\frac{1-x_j-x_j^k}{-1-kx_j^{k-1}}$.

-- Сб ноя 06, 2010 01:15:10 --

Там сходимость очень быстрая.

[Ales]

$x_1=1-\frac 1 {k+1}$
$x_2=1-\frac 1 {k+1}-\frac{\frac 1 {k+1}+(1-\frac 1 {k+1})^k}{1+k(1-\frac 1 {k+1})^{k-1}}$

$x_2=1-\frac 1 {k+1}-\frac 1{k+e}$, $e$ - основание натурального логарифма
...
Возможно, что:
$x=1-\frac 1 {k+1}-\frac 1{k+e}-\frac 1{k+e^2}-\frac 1{k+e^3}-....$

[Хорхе]

1) вообще, априори, это, может быть, и быстрая сходимость. Но если $k=10^8$, то надо взять штук тридцать членов. А чтобы не потерять точность при возведении в степень $n$, надо еще штук сорок, наверное (впрочем, это лучше, чем мое разложение в логарифмами).

2) при замене $(1+\frac1k)^k$ на $e$ точность тоже падает (снова напоминаю, что возводить надо в высокую степень).

[Padawan]

Maple дает такую асимптотику для $x_k$

$$x_k=1-\frac{w(k)}{k}+\frac{1}{2}\frac{w^3(k)}{1+w(k)}\frac{1}{k^2}+O(\frac{1}{k^3}) \ ,$$

где $w(k)=\mathrm{LambertW}\,(k)$ -- корень уравнения $we^w=k$. $w(k)\approx \ln k$.

Только, вроде, остаточный член надо заменить на $O(\frac{1}{k^{3-\varepsilon}})$ с любым $\varepsilon>0$.

[Хорхе]

Ага, по крайней мере можно написать нечто в терминах функции Ламберта.

Но в терминах логарифмов не выйдет, поскольку вот это:

Padawan в сообщении #371217 писал(а):

$w(k)\approx \ln k$.

хоть и правильно, но имеет намного худший порядок аппроксимации, нежели остаточный член в формуле, выданной Maple'ом. Там получится в точности, как я написал, разложение, -- чрезвычайно медленно сходящееся.

Тут еще разложения есть. Может, что и подойдет.