помогите решить пожалйуста.

[Marsel]

Докажите, что существует единственная непрерывная функция, удовлетворяющая функциональному уравнению
$f(2x)=f(x)*(e ^{-x})*cos({($$\pi*x)\over3})$
$f(0)=1$
нужно для начала найти такую функцию...

[ИСН]

Такие формулировочки часто кончаются тем, что функцию хрен найдёшь, хотя она и есть. Но Вам повезло.
Выразите $f(x)$ через $f({x\over 2})$.

[paha]

Искать не надо.

Посмотрите, где она в ноль должна обращаться. Запомните. Потом предположите, что таких функций две и ищите их отношение. Кстати. полезно сделать замену $f(x)=e^{-x}g(x)$

[ИСН]

Обычно да, не надо, но если можно найти, то почему бы не?

[Marsel]

еще нужно по условию этой задачи (пункт б) найти эту функцию, и построить её эскиз....
ну построить график это не проблема, главное найти её....

-- Чт сен 30, 2010 21:15:11 --

предположим я выражу $f(x)$ через $f(x/2)$
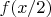
что дальше?

-- Чт сен 30, 2010 21:20:07 --

хотя я немного не понял вашего совета...
как мне выразить $f(x)$ через $f(x/2)$?
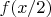
это ведь неизвестная функция.....или я что-то не так понимаю?

-- Чт сен 30, 2010 21:21:40 --

хотя я немного не понял вашего совета...
как мне выразить $f(x)$ через $f(x/2)$?
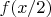
это ведь неизвестная функция.....или я что-то не так понимаю?

[ИСН]

Да, неизвестная. Но кое-что о ней известно: вот уравнение. Вот через него-то и надо...

[Marsel]

выразил...
а дальше как?
в чем заключается идея поиса этой функции?

[ИСН]

Теперь выразите $f(x)$ через $f({x\over 4})$.

[Marsel]

а дальше?

[ИСН]

Дальше выразите $f(x)$ через $f({x\over 8})$.

[Marsel]

то есть я правильно вас понимаю?
и так мы продолжаем до бесконечности....
в итоге первое слагаемое у нас как раз будет $f(0)=1$ (на бесконечности)...а остальные сомножители нам дадут искомую функцию?

[ИСН]

Слагаемое - это когда складывают. В остальном да, всё так и есть.

[Marsel]

ой.....ошибся....первый сомножитель конечно же.

-- Чт сен 30, 2010 22:03:37 --

спасибо огромное=)))

-- Чт сен 30, 2010 22:42:34 --

грубо говоря получилось след:
$cos(A)*cos(2A)*cos(3A)*...*cos(nA)=? $где A - некое выражение.
как посчитать такое произведение?

-- Чт сен 30, 2010 22:42:57 --

грубо говоря получилось след:
$cos(A)*cos(2A)*cos(3A)*...*cos(nA)=?$где A - некое выражение.
как посчитать такое произведение?

[Alexey1]

Используйте равенство $\frac{\sin(x)}{x}=\prod_{j=1}^{\infty} \cos(\frac{x}{2^j})$.

[zhoraster]

Тема перемещена в Карантин

Marsel, формулы надо оформлять в ТеХе. Прочтите как минимум вот это. Звездочки Ваши никому не нужны, уберите их.

Не забудьте поправить заголовок и первое сообщение: думаю, $Pi$ --- это вряд ли произведение числа $P$ и мнимой единицы, а выглядит именно так.

Alexey1, предупреждение (пока устное) за ответ на вопрос, который не был как следует оформлен.