...Вы просто заменили выражение "

" на его определение через понятие "непрерывность": "при доопределении

" функция

становится непрерывной в

".
Чисто формально, если уже определена непрерывность функции в точке через открытые множества, то действительно можно дать определение предела функции в точке через непрерывность.
Определение. Число

называется пределом функции

при

, если функция

непрерывна в точке

Я бы не стал возвращаться к этому разговору, если бы не обнаружил, что практически без изменений это определение годится для определения предела в точке в любых топологических пространствах.
Определение. Пусть дано отображение

:
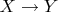
топологического пространства

в топологическое пространство

. Элемент

называется пределом отображения

:
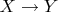
в точке

если отображение

непрерывно в точке

.
Это определение смотрится эквивалентным определению предела по фильтру, если рассматривать предел только по фильтру проколотых окрестностей точки

.
Думаю, что не лишним будет здесь упомянуть соображения
terminator-II о том, что пределы могут быть различны при различных фильтрах:
Берем функцию

при

и

. Если взять фильтр сходящийся к нулю и содержащий множество

, то предел функции по такому фильтру будет равен 1. Если взять фильтр сходящийся к нулю и содержащий проколотые окрестности нуля, то предел по такому фильтру будет равен 0.
...мы можем рассмотреть предел функции по трём различным фильтрам.
1. Фильтр с базой из проколотых окрестностей нуля.
Это классическая ситуация соответствующая определению предела при

. База соответствующего фильтра в множестве значений состоит из множеств {0} и {0, 1}. Предел равен нулю.
2. Фильтр с базой {0}. Это ситуация псевдоопределения предела без ограничения

. База соответствующего фильтра в множестве значений состоит из множеств {1} и {0, 1}. Предел равен единице. Фильтр как бы говорит: «мне безразлично, что там вокруг нуля. В нуле значение единица!».
3. Фильтр всех окрестностей нуля. База соответствующего фильтра в множестве значений состоит из множества {0, 1}. Предел функции по этому фильтру не существует! Фильтр как бы говорит: «противоречие между стремлением и результатом».
Новое определение соответствует только первому случаю.