Найти количество решений уравнения x^2=1 в кольце Z_m

[Leox]

Найти количество решений уравнения $x^2=1$ в кольце $\mathbb{Z}_m,$ если:

$m=p^k,$ $p$ $--$ простое;

$m=2^k,$

$m=p_1^{k_1} p_2^{k_2} \cdots p_n^{k_n}$ для $k, k_i>0,$ $p_i>2.$

[Sonic86]

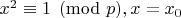
Если $m=p^k$ и $p>2$, то решения два. Чтобы их найти, можно найти 2 решения сравнения $x^2 \equiv 1 \pmod p, x=x_0$, а потом подстановкой $x_{k+1}=x_k+q_kp^k$, решая линейные уравнения. При $m=2^k, k>2$ будет 4 решения.
Случай $m=p_1^{k_1}...p_n^{k_n}, p_j>2$ равносилен системе $x^2 \equiv 1 \pmod {p_j^{k_j}}$, решения которой из случая выше, а потом каждой энке решений соответствует своя линейная комбинация решений, и тогда $N(x^2 \equiv 1 \pmod m)=\prod\limits_{j=1}^nN(x^2 \equiv 1 \pmod {p_j^{k_j}})$.
Вроде бы так

Можно посмотреть Бухштаба, Айрленда с Роузеном и Боревича с Шафаревичем про $p$-адические числа.

[Leox]

Cпасибо, посмотрю ети книги.