Int(0_(pi/2)): ln(cosx)

[Xoma]

Помогите пожалуйста найти Int(0_(pi/2)): ln(cosx) 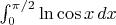$\int_0^{\pi/2}\ln\cos x\,dx$ (2353(б) в Демидовиче)
Уже который день пытаюсь ничего не получается
пробовал по частям,не получается.Учитель сказал сделать замену x=2t,а что собственно дальше?
пробовал расписывать по cos-у двойного угла то-же не получается
видел решение с sin-ом пробовал так же тоже не получается
И еще кто-нибудь знает почему инт-л с sin-ом = инт-лу с cos-ом?
Заранее благодарен за ответы

от модератора AD:

Формулы пишутся вот так.
В следующий раз будет карантин.

[AD]

Xoma в сообщении #320723 писал(а):

И еще кто-нибудь знает почему инт-л с sin-ом = инт-лу с cos-ом?

Вы верите в привиедения? А в замену переменной $x\leftrightarrow \frac{\pi}2-x$?
Собственно, в сочетании с той заменой, которую советовал преподаватель, это и даёт ответ.
Бойан короче.

[Xoma]

т.е просто сделать его инт-ом с синусом?
как 2*Int(pi/2_0):ln(sin(2t)) ?
я вроде так пробовал не получилось

[ИСН]

Что помешало? На пути возник ангел с огненным мечом?

[AD]

Карантин, как и было предсказано. Запишите формулу в $\TeX$е на этот раз сами. Введение здесь. Как справитесь - пишите сюда, и кто-нибудь из модераторов вернёт тему.