Если часы наблюдателя в точке (А) показывают «нуль», то часы наблюдателя точки (В) показывают время не равное нулю, и наоборот. Из-за этого, частицы могут сближаться на минимальное расстояние, но не совмещаться. Мировые линии частиц не пересекаются.
СТО рассматривает, в том числе, движение
точечных частиц. Абстрактные наблюдатели в точке А и в точке В вполне могут быть точечными. Если они движутся друг по отношению к другу, то расстояние между ними (с точки зрения любого из них) меняется со временем. Точечность и движение приводят к тому, что нет никаких препятствий ситуации, когда в некторый момент времени (по часам какого-либо из этих двух наблюдателей) точки А и В совпадут. Если же рассмотреть формулы преобразования Лоренца, учесть, что скорости движения одного наблюдателя с точки зрения второго связаны соотношением
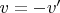
, а совпадение точек означает равенство их пространственных координат, то легко убедиться (сделайте это самостоятельно), что при этом совпадают и показания часов обоих наблюдателей (

). Совпадение всех четрырех координат означает пересечение мировых линий наблюдателей (частиц).
Разумеется, если в произвольный момент времени по часам любого из наблюдателей точки А и В не совпадают, а относительная скорость движения наблюдателей равна нулю, то мировые линии не пересекутся - равенство нулю относительной скорости означает, что мировые линии обоих наблюдателей параллельны, а несовпадение их в одной точке равносильно несовпадению в любой точке (аксиома параллельных соблюдается и в пространстве Минковского). На непересечение мировых линий в такой ситуации уже указал
EEater.
Но если Вы,
stary, сомневаетесь в
принципиальной возможности пересечения мировых линий, то для подтверждения своей точки зрения укажите, пожалуйста, для описанной Вами ситуации
Если часы наблюдателя в точке (А) показывают «нуль», то часы наблюдателя точки (В) показывают время не равное нулю, и наоборот. Из-за этого, частицы могут сближаться на минимальное расстояние, но не совмещаться.
значение этого самого "минимального расстояния", на которое могут сблизиться точки А и В. Например, выразите формульно, как значение "минимального расстояния" зависит от параметров точек А и В (укажите те параметры, которые сочтете нужным).
Вы, действительно, верите в то, что существует во вселенной точка, с которой совмещаются все остальные точки пространства, потом вселенная излучается из этой точки?
Я не думаю, что здравомыслящие участники форума, к числу которых, без сомнения, относится
EEater, считают, что из СТО следовали бы подобные утверждения. А что, Вы нашли дословно такое утверждение в литературе по СТО? Видимо, Вы что-то неправильно интерпретировали - например, рассмотрение умозрительного примера относительного движения двух наблюдателей, мировые линии которых совпдают в точке

и почему-то решили, что этими координатами описываются
все точки Мира?