Несобственный интеграл

[evg]

А чтобы не переписывать пример, можно ли решить его так:
Рассмотрим абсолютную сходимость интеграла: $ \int\limits_0^{2} \frac 1 {|\sqrt[3] {(x^3-8)}|} dx=$ \int\limits_0^{2} \frac 1 {\sqrt[3] {(8-x^3)}} dx $ $ при $0 \leqslant x<2$. Рассмотрим функцию $g(x)= \frac 1 {\sqrt[3] {12(2-x)}} dx $ $$; \int\limits_0^{2} \frac 1 {\sqrt[3] {12(2-x)}}} dx=\lim_{a\to 0}(\int\limits_0^{2-a} \frac 1 {\sqrt[3] {12(2-x)}}} dx)=\frac {3 \cdot (2)^{2/3}} {2\sqrt[3] {12}} $ Следовательно этот интеграл сходится. По предельной теореме сравнения:

$$\lim_{x\to 2} \frac {|f(x)|} {g(x)}=\lim_{x\to 2} \frac {\sqrt[3] {12} \cdot \sqrt[3] {2-x}} {|\sqrt[3] {x^3-8}|}=\lim_{x\to 2} \frac {\sqrt[3] {12} \cdot \sqrt[3] {2-x}} {\sqrt[3] {8-x^3}}=1$$

Значит $ \int\limits_0^{2} \frac 1 {|\sqrt[3] {(x^3-8)}|} dx$ сходится, и следовательно сходится $ \int\limits_0^{2} \frac 1 {\sqrt[3] {(x^3-8)}} dx$, причём абсолютно

[paha]

Если Вам очень хочется применить "предельную теорему сравнения", то можно.

Но легче написать одно неравенство

$$ \int\limits_0^{2} \left|\frac 1 {\sqrt[3] {(x^3-8)}}\right|\, dx\le \frac{1}{\sqrt[3]{4}} \int\limits_0^{2}\frac{dx}{\sqrt[3]{2-x}}=\frac{3}{2}$$

(мог и ошибится с $3/2$ -- считал в уме)

[ewert]

paha в сообщении #305350 писал(а):

Но легче написать одно неравенство

Труднее, гораздо труднее. А вот и пример:

paha в сообщении #305350 писал(а):

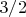
(мог и ошибится с $3/2$ -- считал в уме)

А я даже и не пытался проверять правильность -- ни к чему. Раз всё тривиально определяется именно признаком эквивалентности.

Всегда при доказательствах предпочтительнее использовать идейные приёмы вместо сугубо технических. Во всяком случае -- всегда, когда это проходит.

--------------------------------------------
Хотя да, маленько каюсь. Я там тоже маленько напижонил. Грамотное доказательство такое: $x^3-8\sim C\cdot(x-2)$ при $x\to2$, где $C$ -- это производная того выражения в (единственной) особой точке знаменателя, и она не равна нулю. И всё, и этого вполне достаточно.