Как описать все коммутативные двумерные алгебры над R?

[ellipse]

Как с точностью до изоморфизма описать все ассоциативные коммутативные двумерные алгебры над $\mathbb R$, необязательно с единицей.

Как я понимаю, нужно найти канонический вид структурных констант алгебры в специально подобранном базисе.

Пусть алгебра $A=<x,y>$. Ввиду коммутативности, алгебра определяется 3-мя структурными константами:
$x^2=ax+by$
$y^2=cx+dy$
$xy=ex+fy$
где $a,b,c,d,e,f \in \mathbb R$

Какое нужно сделать преобразование базиса?
Пробовал линейную замену
$x = {\alpha}x'+{\beta}y'$
$y = {\gamma}x'+{\sigma}y'$
но у меня ничего хорошего не получается..

[paha]

Конечно, никаких матриц перечислять не надо... это ж Алгебра!
Напомню, что одномерных алгебр над ${\mathbb R}$ две: само поле $\mathbb{R}$ и алгебра с тривиальным умножением (но нетривиальным умножением на числа!) ${\mathbb R}_0$.

1. Пусть в нашей алгебре $R$ есть идеал $I$, порожденный элементом $u\in R$ (идеал является линейным подпространством, поэтому может быть только одномерным).

По определению идеала $au=f(a)u$ $\forall a\in R$. Нетрудно видеть, что $f:R\to{\mathbb R}$ -- гомоморфизм алгебр.
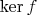
Этот гомоморфизм имеет ядро $\ker f$ -- идеал (какой-то) нашей алгебры

1а) Если $ker f\ne I$, то $R=I\oplus \ker f$ что изоморфно либо ${\mathbb R}\oplus{\mathbb R}_0$, либо $\simeq {\mathbb R}\oplus{\mathbb R}$.
2 алгебры

1б) $\ker f=I$, тогда $u^2=0$, $au=f(a)u$... Найдите идемпотент, т.е. такой элемент $a\in R$, что $a^2=a$. Элементы $u,a\in R$ образуют базис с соотношениями $a^2=a$, $au=u$, $u^2=0$
1 алгебра

1в) $ker f=R$ (интересный случай!) тут $ua=0$ $\forall a\in R$. Начните с того, что $a^2=x_au+y_aa$. Ищите такой элемент $a\in R$, что $x_ay_a=0$.
Тут получится либо ${\mathbb R}_0\oplus{\mathbb R}_0$, либо нильпотентная алгебра $\{e_1^2=e_1e_2=0,e_2^2=e_1\}$, либо уже полученная нами ${\mathbb R}\oplus{\mathbb R}_0$
еще 2 алгебры

2) Идеалов нет -> делителей нуля нет -> любое линейное уравнение разрешимо (применить отрицание существования идеала) -> есть единица -> существует элемент с квадратом равным минус единице-> $R\simeq\mathbb{C}$
еще 1 алгебра... поле)

Всего 6 алгебр

Можно и такой способ: умножение - линейное преобразование плоскости, поэтому алгебра порождена двумя коммутирующими линейными отображениями ${\mathbb R}^2\to{\mathbb R}^2$ (алгебра как свой правый модуль)

линейные отображения коммутируют, если либо одно из них гомотетия, либо если собственные подпространства совпадают... и т.д.

[ellipse]

paha в сообщении #304302 писал(а):

Конечно, никаких матриц перечислять не надо... это ж Алгебра!
Напомню, что одномерных алгебр над ${\mathbb R}$ две: само поле $\mathbb{R}$ и алгебра с тривиальным умножением (но нетривиальным умножением на числа!) ${\mathbb R}_0$.

а это как показать?

Пусть алгебра $R=<u>$
$u^2 + {\alpha}u=0$
${u'}^2=(u+{\alpha}/2)^2= -{{\alpha}^2}/4$. А потом показать, что случаи ${\alpha}=0$ и ${\alpha}<>0$ не изоморфны? Правильно?

Цитата:

1а) Если $ker f\ne I$, то $R=I\oplus \ker f$

почему так?

-- Вт мар 30, 2010 23:39:24 --

paha в сообщении #304302 писал(а):

1б) $\ker f=I$, тогда $u^2=0$, $au=f(a)u$... Найдите идемпотент, т.е. такой элемент $a\in R$, что $a^2=a$. Элементы $u,a\in R$ образуют базис с соотношениями $a^2=a$, $au=u$, $u^2=0$
1 алгебра

Понимаю, что такой элемент $a$ не лежит в подпространстве $\ker f=I$ и поэтому вместе с $u$ образует базис, но не совсем понятно, как его найти.

-- Вт мар 30, 2010 23:43:16 --

paha в сообщении #304302 писал(а):

есть единица -> существует элемент с квадратом равным минус единице

почему?

[ellipse]

Цитата:

Идеалов нет -> делителей нуля нет

Цитата:

делителей нуля нет -> любое линейное уравнение разрешимо (применить отрицание существования идеала)

тоже не могу понять как следует

[paha]

ellipse в сообщении #304707 писал(а):

а это как показать?

Пусть $u^2=\alpha u$. Если $\alpha\ne 0$, то $e=u/\alpha$ -- единица. Если $\alpha=0$, то умножение в алгебре тривиально.

ellipse в сообщении #304707 писал(а):

почему так?

Два выделенных одномерных подпространства, поэтому разложение любого в сумму "идеального" вектора и "ядерного" однозначно, поэтому прямая сумма

ellipse в сообщении #304707 писал(а):

Понимаю, что такой элемент $a$ не лежит в подпространстве $\ker f=I$ и поэтому вместе с $u$ образует базис, но не совсем понятно, как его найти.

Правильно. Начните с какого-то $b\not\in I$, и пусть $b^2=xb+yu$.
Ищем идемпотент:$a=pb+qu$, т.е. решаем относительно $p,q\in{\mathbb R}$ уравнение $(pb+qu)^2=pb+qu$ с параметрами $x,y\in {\mathbb R}$
(не забудете, что $x=f(b)$?).

ellipse в сообщении #304739 писал(а):

Цитата:
Идеалов нет -> делителей нуля нет

это даже подсказывать не буду - читайте определения

ellipse в сообщении #304739 писал(а):

применить отрицание существования идеала

вот отрицание (в двумерной алгебре): $\forall u\ne 0$ $\exists a$ что $u,ua$ -- линейно независимы
ищем решение уравнения $ub=c$ в виде $b=xu+yua$
критическое обстоятельство состоит в том, что $u^2$ и $u^2a$ линейно независимы из-за

ellipse в сообщении #304739 писал(а):

делителей нуля нет

ellipse в сообщении #304707 писал(а):

есть единица -> существует элемент с квадратом равным минус единице
почему?

$(xe+yu)^2=pe+qu$ --- выбором $x,y$ убейте $q$ и посмотрите каким при этом станет $p$.

[ellipse]

paha, спасибо. с делителями нуля кажется разобрался и даже появилась идея доказывать так: Допустим $A$ не содержит собственных идеалов и уравнение $ax=b$ не имеет решений, тогда мн-во $\{ax | x \in A\}$ будет собственным главным идеалом, что невозможно. Правильное рассуждение?

paha в сообщении #304744 писал(а):

Правильно. Начните с какого-то $b\not\in I$, и пусть $b^2=xb+yu$.
Ищем идемпотент:$a=pb+qu$, т.е. решаем относительно $p,q\in{\mathbb R}$ уравнение $(pb+qu)^2=pb+qu$ с параметрами $x,y\in {\mathbb R}$
(не забудете, что $x=f(b)$?).

$p^2b^2+2pqbu+b^2u^2=pb+qu$
$p^2(xb+yu)+2pqbu+0 = pb+qu$
и что дальше? почему $x=f(b)$? пожалуйста, поясните подробнее на этом одном примере. я не понимаю в чем цель и идея этих преобразований

[paha]

ellipse в сообщении #305040 писал(а):

не содержит собственных идеалов

идеал по определению не совпадает со всем кольцом (алгеброй)

ellipse в сообщении #305040 писал(а):

уравнение $ax=b$ не имеет решений, тогда мн-во $\{ax | x \in A\}$ будет собственным главным идеалом

расставьте кванторы, а то я не пойму утверждения)

ellipse в сообщении #305040 писал(а):

и что дальше?

дальше $bu=f(b)u$

ellipse в сообщении #305040 писал(а):

почему $x=f(b)$

$f$ -- гомоморфизм алгебр