К вопросу о бесконечномерности и выделенности.
Я говорил только про бесконечность, про выделенность это вы уже сами добавили. Помимо проcтранств с метрикой Бервальда-Моора бесконечными конформными группами обладают еще многие многомерные плоские финслеровы пространства, в частности, связанные с алгебрами, получаемыми как прямые суммы нескольких комплексных алгебр.
По моим подсчетам, метрика БМ, обладает четырехкратной "предконформной" инвариантностью, без всяких Коши-Риманов и перемешиваний координат. Конформный фактор, есть просто произведение четырех функций, производных, каждая разной одной переменной(точнее корень из них четвертой степени).
Так у двумерного псевдоевклидова пространства все обстоит точно так же как у четырехмерного пространства с метрикой Бервальда-Моора, с той разницей, что вместо четырехкратной "предкомформной" инвариантности тут двухкратная, а конформный фактор есть просто произведение двух функций, производных, каждая разной одной переменной (точнее корень из них второй степени). Что бы увидеть это достаточно перейти из ортонормированного базиса в базис из пары векторов, лежащих на световом конусе псевдоевклидовой плоскости.
То, что вы называете в двумерном псевдоевклидовом случае "перемешиванием" - просто следствие перехода от изотропного базиса к ортонормированному.
Так что или надо доказывать смешивание четырех координат БМ при конформных преобразованиях и многомерные Коши-Римана или никакой выделенности.
Если от изотропного базиса четырехмерного пространства Бервальда-Моора перейти к финслерову аналогу ортонормированного базиса, тут будет "перемешивание" не слабее, чем при аналогичном переходе в двумерном случае.
Выписать многомерные гиперболические условия Коши-Римана для четырех скалярных функций

задающих

-аналитические функции

от
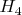
-чисел

(

- гиперболические мнимые единицы, такие что

)
и как они выглядят в финслерово ортонормированном базисе нет никаких проблем:




Легко видеть как при переходе от четырехмерного случая к двумерному остаются обычные гиперболические условия Коши-Римана для двумерного Бервальда-Моора в ортонормированном базисе:


Давайте не говорить про выделенность, мне пока достаточно, что бы вы признали, что конформная группа четырехмерного Бервальда-Моора, как бы просто связанные с нею преобразования в некоторых базисах не выглядели, ровно ничем не "хуже" конформной группы двумерного Бервальда-Моора (он же псевдоевклидова плоскость), которая, кстати, является подгруппой первой.