Пусть

где

Можно ли производную от

считать по обычным правилам дифференцирования интеграла, зависящего от параметра? То есть
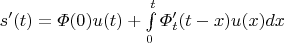
Можно. Хотя бы потому, что это можно делать для дельта-функций, заменённых на дельтообразные последовательности, а потом сделать предельный переход.