Судя по всему ответ будет
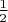
если

нечетно (количество часов в сутках) иначе

Причем вероятность больше быть ближе к часовой стелке меньше.
Для обычных часов получаем

и
 Sasha2
Sasha2
Как-то странно пытаться придраться к условию задачи. Оборот
Цитата:
при случайном взгляде на часы
можно формализовать как много наблюдений за большой период времени (год скажем), но любому нормальному школьнику ясно, что достаточно рассмотреть период системы, т.е. промежуток времени через которой состояние системвы повторит исходное и найти ответ для него.
Цитата:
Ну в этом случае вообще все просто, тогда пространство событий определяется множеством всех углов, которые могут образовывать минутная и часовая стрелка и множеством всех радиусов (точнее их декартовым произведением). Если немножко поднапрячься, то опять же это множество легко разбивается на два равномощных, из которых первое - это те, где секндная ближе к часовой, а второе - то, где наоборот.
Ну пространство Вы определили, а вот меру на нем не подсчитали.