Просто в случае

проще явно найти замкнутый маршрут, чем доказать его существование.
А вообще для существования замкнутого маршрута на доске
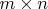
, где

, необходимым и достаточным является выполнение следующих трёх условий:
1)

не является нечётным числом, большим

;
2) при

обязательно

,

3) при

обязательно

Разбор некоторых отдельных случаев см. по второй ссылке выше.