Теория кодирования (реализовать код Хэмминга)

[Xaositect]

Так.
Регистр длины $L$ над полем $F$ это вот такая штука:

То есть на каждом такте мы вычисляем новое $S_0(t+1) = \sum_{i=0}^{L-1} a_i\dot S_i(t)$, а остальные просто сдвигаем: $S_{i+1}(t+1) = S_i(t)$.

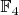
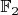
Теперь рассмотрим наш случай. Поле $\mathbb{F}_4$, получающееся расширением поля $\mathbb{F}_2$ корнем многочлена $x^2 + x + 1$
Элементы этого поля имею вид $c = c_0 + c_1\alpha$, где $c_i\in \mathbb{F}_2$, т.е. биты, а $\alpha$ - корень многочлена $x^2 + x + 1$. Складываются они по модулю 2, а умножаются как многочлены по модулю $(\mathrm{mod }\ \alpha^2 + \alpha + 1, \mathrm{mod }\ 2)$. То есть мы можем $\alpha^2$ заменить на $\alpha + 1$, потому что $\alpha^2 + \alpha + 1 = 0$. Например:
$(1 + \alpha) + \alpha = 1$
$(\alpha)*(1 + \alpha) = \alpha + \alpha^2 = \alpha + (\alpha + 1) = 1$

Точно так же, если у нас поле $\mathbb{F}_{27}$, полученное расширением $\mathbb{F}_3$ корнем неприводимого многочлена $x^3 + 2x^2 + 1$, от элементы будут иметь вид $c = c_0 + c_1\alpha + c_2\alpha^2$, где $c_i=0,1,2$, складываться по модулю 3, а умножаться как многочлены с учетом того, что $\alpha^3 = -(2\alpha^2 + 1) = \alpha^2 + 2$.
Например:
$(1+\alpha^2)(1+\alpha^2) = 1 + 2\alpha^2 + \alpha^4 = 1 + 2\alpha^2 + \alpha(\alpha^2 + 2) = 1 + 2\alpha + \alpha^2 + \alpha^3 = 1 + 2\alpha + \alpha^2 + (\alpha^2 + 2) = 2\alpha + 2\alpha^2$

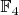
Все коэффициенты $a_i$ и значения регистра $S_i$ - будут элементами нашего поля, т.е в случае $\mathbb{F}_4$ - это пары бит, а в случае $\mathbb{F}_5$ - числа от 0 до 4 с арифметикой по модулю 5.
Кстати, обычно считается, что $a_0=1$ или хотя бы $\neq 0$