natalya_1Поэтому путь неравенств и интервалов лучше оставьте. Там ловить нечего.

Проверять не буду, предоставлю эту возможность другим.
Но я не шла путем неравенств и интервалов.
Обращаюсь к другим участникам форума: пожалуйста, посмотрите доказательство.
Здравствуйте, уважаемые форумчане! Представляю на Ваш суд свою попытку доказательства БТФ. Буду благодарна за критику.
Доказательство буду выкладывать по частям . Положения, помеченные *** требуют отдельных доказательств , они достаточно простые, поэтому я не стала их здесь приводить, чтобы не перегружать сильно сообщение. Если нужно, я их выложу. Прошу так же извинить меня за то, что не смогла там, где надо, показать системы уравнений, не получилось набрать.
Итак, Ферма утверждал, что уравнение

не имеет целочисленных решений при

. Попробуем доказать обратное.
1.1. Предположим, что такое решение существует, при

,

,

,
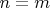
, где

,

,

- целые положительные взаимнопростые числа,

, пусть

,

- целое число >2.
Тогда

.
1.2.

, где

- целое положительное число.***

, где

-целое положительное число.***
1.3.

,

Перемножаем левые и правые части, получаем:

,

,

,

,

.***
1.4.

,

(п.1.1). Перемножаем левые и правые части, получаем:

, следовательно,

.
Левая часть равенства представляет собой значение функции

при

, а правая - при

, взятое с противоположным знаком.
Равенство будет выполняться в двух случаях:
1.4.1.если значение функции при

и

равно 0.
или 1.4.2.если функция в точках

и

принимает одинаковые значения разных знаков.
Рассмотрим каждый из случаев.
1.5.. Пусть

,

, тогда

,

, (

,

,

(п.1.3)), следовательно,

1.6. Исследуем функцию

.

,

,

-точка разрыва.
Найдем точки экстремума:


.

или

,

,

Так как на сегменте
![$]0;c]$ $]0;c]$](https://dxdy-02.korotkov.co.uk/f/1/6/c/16c732884e0dd3c035ebcffddad83d4d82.png)
существует только одна точка экстремума, первый вариант(1.4.1) невозможен.
2.1. Рассмотрим второй возможный вариант.
Итак,

Преобразуем выражение, получаем:

. Числитель правой части делится на

, знаменатель- на

. Поскольку

, то

, где

- общий делитель

и

***
2.2.Следовательно, необходимо сократить числитель на

.

и

сокращаются на

между собой ***, поэтому дальнейшее сокращение будет невозможным.

и

сокращаются на

,

сокращается на

.

не сокращается, т.к.

и

-взаимно простые числа.
Следовательно, сократить числитель на

невозможно. Аналогично с сокращением знаменателя.
Следовательно,

и

могут быть равны только

, а это невозможно, т.к.
