Понятие арифметического корня в случаях
![$\sqrt[2n]{a}=b$ $\sqrt[2n]{a}=b$](https://dxdy-04.korotkov.co.uk/f/f/b/1/fb1e574ad9fdd1357c48dbf4bcc41ab182.png)
необходимо заменить на знак модуля, потому что такой ответ выглядит неполным, так как есть отрицательный корень "
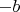
" .
Правильно,
![$| \sqrt[2n]{a} |=b$ $| \sqrt[2n]{a} |=b$](https://dxdy-03.korotkov.co.uk/f/2/f/9/2f951c1934cdde1f2bfe6e544b63857882.png)
.
Необходимо обозначить специальным знаком случаи,когда из
![$\sqrt[2n]{a}$ $\sqrt[2n]{a}$](https://dxdy-04.korotkov.co.uk/f/7/2/d/72d64455c8b1a043fde65aa0e6b0fc9d82.png)
берутся только отрицательные значения.
Как насчёт,обозначить
![$|| \sqrt[2n]{a} ||=-b$ $|| \sqrt[2n]{a} ||=-b$](https://dxdy-01.korotkov.co.uk/f/c/8/5/c85869c5809791867e8ab334638fcab582.png)
.
Здесь

- целое число.