Точность оценки погрешности интерполяции

[ewert]

Ну и пусть себе обращается -- просто опустите горизонтальный участок на ось непрерывной деформацией. И что?...

[TOTAL]

ewert в сообщении #237003 писал(а):

Ну и пусть себе обращается -- просто опустите горизонтальный участок на ось непрерывной деформацией. И что?...

Просто вспомните, что речь идет о $R^{(n-1)},$ которая равна тождественно нулю между двумя своими нулями и всюду МОНОТОННА. Тогда $R^{(n-2)}$ равна нулю между тремя своими нулями и НЕ МЕНЯЕТ ЗНАК и т.д.

[ewert]

TOTAL в сообщении #237010 писал(а):

Просто вспомните, что речь идет о $R^{(n-1)},$ которая равна тождественно нулю между двумя своими нулями и всюду МОНОТОННА. Тогда $R^{(n-2)}$ равна нулю между тремя своими нулями и НЕ МЕНЯЕТ ЗНАК и т.д.

А почему, собственно, $R^{(n-2)}$ не меняет знак? И к., собственно, д.?

И вообще: не могли бы Вы собрать всё вместе? Пока что я вижу лишь намёки, и даже непонятно, в какую сторону их домысливать.

[gris]

ewert писал(а):

Там ведь три узла. Хоть на одной из двух частей интервала функция не постоянна, поэтому там есть две точки, в которых первая производная принимает значения разных знаков. А в оставшейся части заведомо есть точка, в которой первая производная обращается в ноль.

И она лежит по одну сторону от тех двух. То есть по Лагранжу вторая производная принимает и положительные и отрицательные значения.
Увы, летний отдых даром не прошёл.

[TOTAL]

ewert в сообщении #237019 писал(а):

А почему, собственно, $R^{(n-2)}$ не меняет знак? И к., собственно, д.?

И вообще: не могли бы Вы собрать всё вместе? Пока что я вижу лишь намёки, и даже непонятно, в какую сторону их домысливать.

Ничего не надо домысливать, это полное решение.

Из предположения, что $R^{(n)}(x)$ всюду не меняет знак (для определенности неотрицательна) и обращается в ноль при $x^{(n)}_0б$ следует, что $R^{(n-1)}(x)$ обращается в ноль между двумя своими корнями $x^{(n-1)}_0$ и $x^{(n-1)}_1$ (между которыми лежит $x^{(n)}_0$) и не убывает на остальной части отрезка.

Из того, что $R^{(n-1)}(x)$ обращается в ноль между двумя своими корнями $x^{(n-1)}_0$ и $x^{(n-1)}_1$ и не убывает на остальной части отрезка, следует, что $R^{(n-2)}(x)$ обращается в ноль между тремя своими корнями $x^{(n-2)}_0$ и $x^{(n-2)}_2$ и неотрицательна на остальной части отрезка.

И так далее. В итоге получаем, что из предположения, что $R^{(n)}(x)$ всюду не меняет знак и обращается в ноль при $x^{(n)}_0,$ следует, что $R^{(0)}(x)$ равна нулю на всем отрезке.

[gris]

TOTAL,то есть если дважды дифференцируемая функция равна нулю на концах отрезка, её первая производная неубывает и равна нулю на одном из концов отрезка, то функция на этом отрезке тождественно равна нулю.

Наглядно мне понятно, что функция не может быть выпуклой в одну сторону, но вот простое доказательство не очевидно сразу Через Лагранжа и противоречие?

[ewert]

Ну теперь, пожалуй, можно считать это доказательством (в смысле ошибок я так сходу не вижу).
Хотя немножко корявым. Я изложил бы примерно ту же идею несколько иначе. Общий смысл: для двух узлов утверждение верно, а дальше -- индукция по количеству узлов (для первой производной гарантировано существование на единичку меньшего к-ва узлов и, следовательно, по предположению доказываемое утв. для неё справедливо и т.д). Правда, корни производной на крайних отрезках надо выбирать не абы как, а, соответственно -- наименьший и наибольший.

А предполагалось совсем другое доказательство, и действительно полное.

Для произвольной функции $g(x)$ набор точек $t_1<t_2<\ldots<t_m$, $m\geqslant2$, назовём квазиальтернансом, если $g(t_k)=(-1)^k\alpha_k$, где или все $\alpha_k\leqslant0$, или все $\alpha_k\geqslant0$.
Точку квазиальтернанса назовём строгой, если для неё $\alpha_k\neq0$.
Квазиальтернанс назовём невырожденным, если у него не менее двух строгих точек.

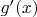
Утверждение 1. Если на некотором интервале $(a;b)$ функция $g(x)$ имеет невырожденный квазиальтернанс из $m$ точек ($m\geqslant3$), то её производная $g'(x)$ имеет на этом же интервале невырожденный квазиальтернанс из $(m-1)$ точки.
(Достаточно на каждом интервале $(t_{i};t_{i+1})$ выбрать точку $t'_i$, для которой справедлива формула Лагранжа. Эти точки образуют, очевидно, квазиальтернанс для производной, и притом невырожденный: если хотя бы одна строгая точка прежнего квазиальтернанса была внутренней, то она уже порождает две строгих точки нового, а если строгими являлись две крайних точки, то каждая из них порождает одну строгую новую точку.)

Утверждение 2. Пусть функция $f(x)$ обращается в ноль в каждом из узлов $x_0<x_1<\ldots<x_n$, $\ n\geqslant1$, причём $f(x)\not\equiv0$ на всём $[x_0;x_n]$. Тогда её производная $f'(x)$ имеет на интервале $(x_0;x_n)$ невырожденный квазиальтернанс из $(n+1)$ точки.
(На хотя бы одном из интервалов $(x_{i-1};x_{i})$ функция не равна константе. Из теоремы Лагранжа следует, что внутри этого интервала найдутся две точки, в которых производная не равна нулю и принимает значения разных знаков. Недостающие $(n-1)$ точку квазиальтернанса можно получить, взяв, например, по одной точке внутри каждого из остальных интервалов, в которой производная обращается в ноль.)

Следствие. В условиях утверждения 2 производная $f^{(n)}(x)$ имеет на интервале $(x_0;x_n)$ невырожденный квазиальтернанс из двух точек.
Т.е. существуют две точки, в которых $f^{(n)}$ принимает значения разных знаков. Что, собственно, и требовалось.