Прежде, чем продолжить (так сказать, "на берегу") хочу высказать публично одно пожелание:
Уважаемый maxal! В случае, если доказательство покажется Вам убедительным, учитывая Вашу неоценимую помощь мне в предшествующие годы, сочту за Честь, если Вы согласитесь продолжить работу над ним на правах соавтора.Для дальнейшего доказательства рассмотрим числовую ось - это прямая линия с нанесенными на ней метками. Каждому целому числу на оси соответствует своя метка.
Случай 1: Четное число

не кратно 3.
На числовой оси от нечетных чисел, кратных 3 и расположенных на промежутке

, проводим синусоиды с полупериодом, равным

, через участки

и

(синусоиды - суть арифметической прогрессии с шагом

).
Количество указанных чисел (соответственно, синусоид) с погрешностью

равно

.
Пересечение синусоид с числовой осью произойдет через метки, соответствующие нечетным числам.
Если

, то на участке
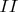
синусоиды пересекут метки нечетных чисел, имеющих остаток

, а на участке

метки нечетных чисел, имеющих остаток

.
Если

, то на участке
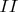
синусоиды пересекут метки нечетных чисел, имеющих остаток

, а на участке

метки нечетных чисел, имеющих остаток

.
Для простого числа 3 выполняется:


Следовательно, каждая из синусоиды пересечет метки нечетных чисел, симметричных относительно 0 и имеющих одинаковый по абсолютной величине остаток по основанию 3.
Таким образом, создать пару, принадлежащую одной синусоиде на интервале

и
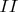
могут только числа, непревышающие по абсолютной величине число

и имеющие одинаковые по абсолютной величине остатки по основанию 3.
Таких нечетных чисел

.
Чтобы хотя бы одно число в каждой из пар было составным, необходимо иметь количество таких чисел, равное количеству синусоид, т.е.

. Но уже при

имеется более пяти штук простых чисел, имеющих одинаковый остаток по основанию 3 (одно из которых может пойти в пару с непростым и несоставным числом 1, еще одна пара может понадобиться для компенсации погрешности +1). Соответственно, количества составных чисел для всех пар не хватает.
Таким образом, при любом

имеется, как минимум, одна пара простых чисел

и

таких, что:

или

.