Задача: в урне очень много шариков, вероятность вытащить красный = 0.6 вероятность белый = 0.4. Найти вероятность того что что два вытащенных щарика будут разного цвета.
A - событие обозначающие что первый шарик красный
B - событие обозначающие что второй шарик красный
очевидно что решение:
A + B - AB
Причем видимо (A+B)-AB .
два вопроса:
1) не могу в учебниках найти про то что

то есть почему ассоциативность

работает только на сложение?
2) Как вычислить вероятность (A+B)-AB ? :
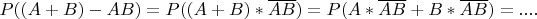
то есть получить формулу для вычисления вероятности которую можно вычислить зная только что P(A)=0.6 и P(B)=0.6 и что эти события независимы.