А, понял.
Добавлено спустя 6 минут 17 секунд:
Вообще вопрос проистекает вот откуда:
Дана система функций. Известно, что она ортогональна на интервале


, а на
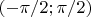
ортогональность со стандартным скалярным произведением для функций уже не работает.
Соответственно, сделать вывод о л/н-з на
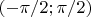
на основании (1) уже нельзя. Как я понимаю.