задачи по теории вероятности. Вопросы в ходе решения.

[Asaru]

в коробке - по 7 жёлтых, синих и красных шаров.
наудачу и без возвращения выбирают 5 шаров.
найти вероятности следующих событий:
1) среди вынутых шаров попадуться не менее 2-х синих шаров
2) среди вынутых шаров попадуться не менее двух синих шаров или не менее трёх красных

решение
$n = 7 + 7 + 7 = 21$

1) от двух до 5 синих шаров

$N$ - число всех равновероятных исходов
$N = C_{21}^5 = 20349$

число благоприятных исходов
$M2 = C_5^2 = 10$
$M3 = C_5^3 = 10$
$M4 = C_5^4 = 5$
$M5 = C_5^5 = 1$

$M = M2*M3*M4*M5 = 500$
(Т.к. эти события совместны: можно ведь вытащить сразу 5 шаров, или нет?)

Или правильно считать их несовместными, и тогда общее число положительных исходов такое:
$M = M2 + M3 + M4 + M5 = 26$

Искомая вероятность:
$P = M/N = 500/20349 = 0.025$
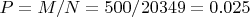
или же (если $M = 26$)
$P = M/N = 26/20349 = 0.0013$

2) среди вынутых шаров попадуться не менее двух синих шаров или не менее трёх красных

Для красных шаров число благоприятных исходов
$M3 = C_5^3 = 10$
$M4 = C_5^4 = 5$
$M5 = C_5^5 = 1$
Соответственно, здесь та же история: можно ли считать эти события совместными, т.е. общее число благоприятных исходов М2 будет: $10 + 5 + 1 = 16$
или $10 * 5 * 1 = 50$

А далее вероятность:
$P = (M1 + М2) / N = 550/20349=0.027$
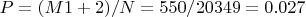
где $M1$ и $M2$- сумма благоприятных исходов для синих и красных шаров соответственно. Формулу сложения я использую потому, что её формулировка: суммой событий А и В называется такое событие, состоящее в наступлении хотя бы одного из них или их вместе. Что как раз необходимо по условию: не менее двух синих шаров или не менее трёх красных.

Я не сильна в этой науке, поэтому, пожалуйста, посмотрите, правильно ли решение?

[gris]

Ошибка. Например: $M2$ - количество вариантов, когда в выборке ровно 2 синих шара. 2 синих из 7 и 3 несиних из 14. То есть надо умножить $C_7^2\cdot C_{14}^3$.
Cобытия несовместны и варианты $M2$,$M3$ ,$M4$ ,$M5$ можно складывать. Идея у Вас правильная. Но проще так - не менее двух это дополнение к событию "вообще нет синих или один синий"

[Евгений Б.]

Я попытаюсь ответить на первую часть вопроса
1) среди вынутых шаров попадутся не менее 2-х синих шаров

возможно, моё решение не совсем рациональное.
как предлагал gris было бы проще.



Я хотя и поставил знак равенства в конце, на самом деле имел ввиду приближённо равно.

А у Вас как-то мало получилось: 1-2 шанса из 100 — это даже навскидку мало.

[gris]

Во втором случае надо внимательно проследить за тем, чтобы не учитывать благоприятные варианты по нескольку раз. Например: 5 красных + 4 красных 1 некрасный + 3 красных 2 некрасных+ 2 красных 3 синих + 2 красных 2 синих 1 жёлтый + 1 красный 2 синих 2 жёлтых ну и тд. Наверное, можно попроще, хотя и тут немного считать на самом деле.

[Asaru]

Разобралась, решила, сдала. Можно было бы показать, но там столько печатать ......
У меня получилось
1) 0,5577
2) 0,64723

Евгений Б., красочно вы всё оформляете.

У меня получилось на половину, как у Евгений Б, а наполовину, как gris советовал вначале.
Последнюю мысль gris тоже поняла:
фактически я также считала "неверные" варианты, а потом отняла их от 1. А можно было сразу посчитать благоприятные.

Спасибо за помощь.

[--mS--]

Оба ответа неверны. Первый должен быть $0,557275542$, второй $0,702786377708978$.

[Архипов]

$P(5)=(1)*7*6*5*4*3/(21*20*19*18*17)$
$P(4)=(5)*7*6*5*4*14/(21*20*19*18*17)$
$P(3)=(10)*7*6*5*14*13/(21*20*19*18*17)$
$P(2)=(10)*7*6*14*13*12/(21*20*19*18*17)$
$P(C>1)=P(2)+...+P(5)=0,557275542$
$P(K>2)=P(3)+...+P(5)=0,181630547$
$P(3K+2C)=(10)*7*6*7*6*5/(21*20*19*18*17)=0,036119711$
$P((C>1) or (K>2)) =P(C>1)+P(K>2) - P(3K+2C) = 0,702786377$

[--mS--]

Не надо ещё вариантов. Правильный ответ указан выше.

[Asaru]

Другую задачу преподаватель смотрит и говорит: у вас тут ответ не сходится (с тем что у него).
Пересмотрел формулы - правильные.
Посчитал на машинке по формулам - правильно.
Я сижу, мучаюсь глобальными мыслями, где же я пропустила число, и большое наверно...
Он мне: тут должно быть 0,217, а у вас 0,264. ОГРОМНАЯ разница.

--mS--, я считала, не ориентируясь на вычисления Евгений Б., но ответы у нас совпали. Также я считала все С 2-мя способами: вручную и через специальную программу.
О правильности ответа мне уже думать не надо, т.к. всё сдано, но всё же интересно: покажите какую-нибудь часть ваших вычислений (лучше вторую).... Может, вы при вычислениях сразу сильно округляли, и ответ потом получился меньше?

[--mS--]

Asaru писал(а):

:P
Другую задачу преподаватель смотрит и говорит: у вас тут ответ не сходится (с тем что у него).
Пересмотрел формулы - правильные.
Посчитал на машинке по формулам - правильно.
Я сижу, мучаюсь глобальными мыслями, где же я пропустила число, и большое наверно...
Он мне: тут должно быть 0,217, а у вас 0,264. ОГРОМНАЯ разница.

Очень жаль, что Вы не видите разницы. Если, скажем, первое число есть правильный ответ, то второе - ответ неверный, решение неверное, так что разница между ними кардинальная.

Asaru писал(а):

--mS--, я считала, не ориентируясь на вычисления Евгений Б., но ответы у нас совпали.

Нет, не совпали.

Asaru писал(а):

Также я считала все С 2-мя способами: вручную и через специальную программу.
О правильности ответа мне уже думать не надо, т.к. всё сдано, но всё же интересно: покажите какую-нибудь часть ваших вычислений (лучше вторую).... Может, вы при вычислениях сразу сильно округляли, и ответ потом получился меньше?

Как только Вы напишете свои вычисления, я покажу, где ошибка. Никак не иначе. Я составляю контрольные не для того, чтобы потом их же и решать
А не хотите писать - не надо.

[Евгений Б.]

--mS-- писал(а):

Оба ответа неверны. Первый должен быть $0,557275542$, второй $0,702786377708978$.

Вы считаете, что неверен ход решения или дело только в цифрах?
$11340/20349 = 0,5572755417957$ если уж быть точнее.

Я ведь написал:

Цитата:

Я хотя и поставил знак равенства в конце, на самом деле имел ввиду приближённо равно.

[--mS--]

Евгений Б. писал(а):

Вы считаете, что неверен ход решения или дело только в цифрах?
$11340/20349 = 0,5572755417957$ если уж быть точнее.

Ваш ответ, разумеется, верен. Неверен ответ $0,5577$. И совсем неверен второй ответ Asaru.

[Asaru]

ладно, напишу

так
$n = 7 + 7 + 7 = 21$

1) от двух до 5 синих шаров

$N$ - число всех равновероятных исходов
$N = C_{21}^5 = 20349$

э.... как тут "не" А сделать? тогда просто цифры напишу, ладно?

$ 0,0983832 + 0,3443412 = 0,4427244$
$ P(A) = 1 - 0,4427244 = 0,5572756$
ну, как видите, я люблю округлять, или, скорее всего, в спешке просто не заметила 2 между 2-мя семёрками

второе условие перепроверю вечером

[--mS--]

Это верно. Да, наверняка в первый раз просто потеряли двойку. А вот Ваше решение (б) неверно.

З.Ы. Надо писать $C_{21}^5$ - наведите мышкой и посмотрите на формулу. Нижний индекс состоит из двух цифр, поэтому взят в фигурные скобки.

[Asaru]

О, понятно. Я пробывала по разному вводить 2 цифры: в обычных скобках и т.д., но было ещё хуже, поэтому схитрила. Сейчас исправлю.

"А вот Ваше решение (б) неверно."

Знаю, что не верно. Уже 4 раз его пересчитываю. Я, конечно, понимаю, что лучше всего посчитать заново так, как мне предлагали выше, но... это же не интересно.

Давайте так: мне всё-таки понятнее через тот же метод, который я использовала в пункте один (т.е. сначала ищем "не А", а потом отнимаем его от единицы)

Не "Б" - это все исходы, которых не должно быть, а именно:
1. Нет синих, нет красных $C_{7}^5 / C_{21}^5$, т.е. я под этим подразумеваю, что все 5 шаров были вытянуты из 7 возможных жёлтых. Если я ошибаюсь уже здесь, то исправьте, если нет, буду писать дальше...