О гипотезе Каталана

[Батороев]

Начинал я эту тему с рассмотрения небольшого частного вопроса, но коль скоро разговор перешел о гипотезе в целом, то изменил название темы.

Гипотеза Каталана утверждает, что уравнение $ x^y - z^t = 1 $ имеет единственное решение $ x=3; y=2; z=2; t=3 $ в натуральных числах, больших единицы.

Для $ z $ - четных и $ x\equiv 3\pmod{4} $ :

Преобразуем:
$ \frac{x^y+1}{2} = \frac{z^t+2}{2} $
Отсюда видно, что при нечетных $y$ равенство не выполнимо, т.к. в левой части - четное число, в правой части - нечетное.

При $ y $ - четном можно записать:
$ z^t = (x^{\frac{y}{2}})^2-1 $.
Отсюда следует, что должны существовать два множителя числа $ z^t = ab $, такие, что $ a-b=2$, что невозможно по следующим причинам:
Если $ a $ и $ b $ - невзаимнопростые, то вынося общие простые делители за скобку, получаем число, большее двух, кроме указанного случая.
Если $ a $ и $ b $ - взаимнопростые, то должно $ a - b = k^t-l^t=2 $, что также невозможно.

[Батороев]

Читая статью про гипотезу Каталана, натолкнулся на такую фразу:

Цитата:

окончательное решение уравнения $ x^2-z^t=1 $ было получено лишь в 1960 году китайским математиком Ко Чао.

В связи с этим возник вопрос - в чем может заключаться некорректность следующих рассуждений?
$ x^2-1=z^t $
Так как в левой части имеем разность квадратов, то должны существовать два множителя числа $ z^t = ab $ такие, что $ a - b = 2 $, что невозможно по двум причинам:
1. Если $ a, b $ - невзаимнопростые, то вынося общие простые делители за скобки, получим число, большее $ 2 $, кроме тривиального случая.
2. Если $ a, b $ - взаимнопростые, то также $ a - b = k^t - l^t > 2 $

На основе данных рассуждений можно было бы сделать вывод о том, что $ y $ в целом в уравнении Каталана $ x^y-z^t=1$ не может быть четным числом.

Добавлено спустя 1 час 14 минут 4 секунды:

Понял, что мои рассуждения годятся только для $z$ нечетных.
Для четных необходимо доказывать, что $ z^t\ne {8T_{\frac{x-1}{2}} $, где $ T_{\frac{x-1}{2}} $ - треугольное число.
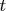
Но в этом случае уже $ t $ не сможет быть четным числом (что тоже неплохо ).

[Sonic86]

Доказано ли для показателей 2 и 3 во всех вариантах?

[Sonic86]

Кстати, показатели можно брать простыми, как в ТФ.

[MaximKat]

Если верить mathworld то она была доказана в 2002 году. Или теперь есть не только ферманьяки, но и каталаньяки?

[Sonic86]

А если верить Кванту за 04.2008, то была доказана в 2003 году румынским математиком П. Михайлеску.
Жаль. А то мне ТФ осточертела.
Правда доказательство неэлементарно, а вдруг есть более простое.
Жаль, он не оставил записи типа: я это доказал, но у меня дома слишком мало перьев, чтобы записать доказательство

[sceptic]

Исчерпывающая информация по истории вопроса (с доказательствами!) - у историка математики Jeanine Daems
A cyclotomic proof of Catalan's conjecture.
У нее же есть более популярная статья (правда, на датском)
Het vermoeden van Catalan - зато с фотографией Михайлеску
Изложение доказательства Михайлеску можно найти в следующих статьях:
1. Yuri F. Bilu, Catalan's conjecture (after Mihailescu)
2. Jacques Boéchat, Maurice Mischler, La conjecture de Catalan racontée á un ami qui a le temps

[maxal]

Фотография Михайлеску есть и в википедии -
там же указаны ссылки на исходное доказательство.

[sceptic]

maxal писал(а):

Фотография Михайлеску есть и в википедии -
там же указаны ссылки на исходное доказательство.

Только по этим ссылкам ничего не дают , и фотография на Википедии - постановочная (на фотографии в статье Jeanine Daems Михайлеску снят врасплох, и потому выглядит более естественным).

[shwedka]

Oригинальную статью Михайлеску забирайте на http://ifolder.ru/8852042
После этого, он немало сделал для уравнения Fermat-Catalan
$x^p+y^p= b z^q$

[sceptic]

С удовольствием добавил статью в свой архив.
Надеюсь, Батороев и Sonic86 тоже обратят внимание на ссылку.
Насчет вклада Михайлеску в уравнение Ферма-Каталана я в курсе.

[Sonic86]

Спасибо большое.
Конечно, доказательство на порядок короче, чем у Уальса.

[sceptic]

Хорошо бы добраться до книги Рибенбойма по сабжу:
Catalan's Conjecture: Are 8 and 9 the Only Consecutive Powers?.
Книга вышла в 1994 г., но что-то никаких следов ее в инете не нашел - не интересна она публике .

О! И Шпрингер порадовал - выходит книжка René Schoof. Catalan's Conjecture.
Ну, ее искать еще рано.

[shwedka]

в более поздней книжке Рибенбойма, 2000 года
которую можно взять, например, на
http://ifolder.ru/8871683
есть большой раздел, этой теме посвященный.

В книге Коена, Теория чисел, 2007-2008 есть большой раздел, посвященный Каталану, но второй еще шпрингер не выложил в доступ. Как только появится, заберу. Так же, как новую книгу о Каталане.

[Sonic86]

Блин, почему же случай $p=2,q=3$ такой сложный?!
Попробовал сам решить.
Если $y^3=x^2-1$, то приходим к уравнению $u^3-2v^3 = \pm 1$, а если брать $x^2=y^3+1$, то приходим к $3u^4-3u^2+1=v^2$.
В обоих случаях я благополучно застрял...