Разумная задача по мотивам того, что написано, имела бы следующий вид. Итак, мы провели 100 испытаний и ни разу не вытащили черный шар. Если обозначить неизвестную вероятность извлечения черного шара через

, тогда вероятность наблюденного нами события равна

. Зададимся "надежностью", скажем, 99%; это означает, что если мы наблюдаем один раз некоторое событие, то будем верить в то, что его вероятность не меньше
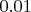
.
Составим уравнение

Решая его, получаем

Таким образом, если

, то вероятность того события, которое мы наблюдали, будет меньше
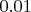
Словами это можно выразить так: с надежностью 99% наш эксперимент показывает, что

.
Это все, что можно сказать. Можно ли отсюда говорить, что черных шаров в корзине нет - решать вам. Скажем, если всего в корзине 10 шаров, тогда такой вывод будет достаточно надежным, поскольку минимальное положительное значение

при этом равно

(и тогда вероятность не получить ни одного черного шара для 100 извлечений равна примерно

).
Если же всего в корзине 100 шаров, тогда такой вывод заведомо не будет надежным, поскольку минимальное положительное значение

равно
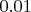
, что укладывается в наши границы. И действительно, если в корзине 1 черный шар на 99 белых, то вероятность ни разу не вытащить черный шар при 100 испытаниях равна примерно

. В том, что наблюдается такое событие, нет ничего удивительного.