Собрал полностью решение....хотелось бы выслушать недочеты...как можно было бы проще решить(только учитывая, что это 11 класс)
1. Рассмотрел подкоренное выражение из второго уравнения.

Далее по теореме Безу установил, что многочлен делится на

Поделил по схеме Горнера и получил

Это выражение должно быть больше или равно нулю. Соответсвенно ОДЗ тогда

и

2. Исследуем первое уравнение.

и

Из всего этого следует, что уравнение имеет только один корень.
Подствляем

в первое уравнение и у нас получается верное числовое равенство, т.е. он и является корнем первого уравнения. (Совершено не понятно с чего бы это вдруг я должен был поствлять это значение в первое уравнение, но он является корнем)
3. Найденное значение подствляем во второе уравнение



Далее рассомрим случаи:



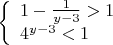
Чего быть не может. Из всего этого следует, что исходная система не имеет нерешений.
P.S. Хотелось бы узнать, как еще можно решить(используя производную к подкоренному выражению, не получалось у меня, может я неправильно что-то использовал). Я понял, что первое уравнение имеет вещественное( не знаю как назвать) решение только вида a\b, где a - целый делитель 15, а b - натуральный делитель 2. Но здесь некоторые товарищи решали, просто подствляя найденное из ОДЗ значения х, и убеждались в правильности найденного корня. То есть меня больше всего волнует, именно нахождения этого корня

... кроме способа описанного выше, можно еще как-нибудь найти корень первого уравнения?