При
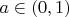
сходится. Короткого и красивого решения не нашёл. Схема доказательства:
Решение "соответствующего дифура"
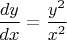
есть функция
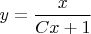
, имеющая конечный предел при

. Что
намекает на асимптотику сходимости последовательности
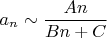
.
Немного повозившись, можно получить оценку
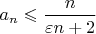
, которая доказывается муторно, но элементарно индукцией (

нужно выбрать так, чтобы база индукции выполнялась).
Численные эксперименты намекают на более точную оценку
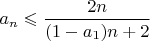
, но, к сожалению, эта оценка индукцией не доказывается.