Вопрос по теории кубита на Джозефсоновском переходе

[naskamejke]

Вот как начинается изложение теории кубита на Джозефсоновском переходе у Mikio Nakahara и Tetsuo Ohmi (в принципе, в других источниках, например у Лихарева, подход аналогичный).
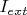
Джозефсоновский переход рассматривается вместе с емкостью $C$ между контактами. Предполагается ток $I_{ext}$, создаваемый внешними источниками.
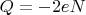
$V$ и $Q$ - напряжение и заряд на контакте. $Q=-2eN$, где $N$ - количество куперовских пар создающих заряд. Уравнения описывающие переход:

$$\dfrac{dQ}{dt}=-I_{ext}+I_c \sin \phi$$

$$\dfrac{d \phi}{dt}=-\dfrac{2eV}{\hbar}$$

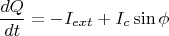
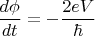
$\phi$ - разность фаз параметра порядка. Все прекрасно. (Знаки немного странно выглядят, не обращайте внимание, там так выбрано).
Далее эти уравнения рассматриваются как уравнения движения которые должны быть получены из лагранжиана/гамильтониана.
Лагранжиан $L=\dfrac{1}{2}\dfrac{C \hbar^2}{4e^2}\left(\dfrac{d\phi}{dt}\right)^2+\dfrac{I_c \hbar}{2e}\cos\phi+I_{ext}\dfrac{\hbar}{2e}\phi$
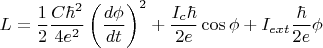
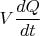
Первый член - электростатическая энергия емкости - полагается кинетической энергией, два следующих члена (с минусом) полагаются потенциальной энергией (этому есть определенное обоснование, производная "потенциальной энергии" по времени есть $V\dfrac{dQ}{dt}$ по крайней мере при постоянном $I_{ext}$)
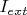
Далее эта теория полагается классической, которую следует проквантовать.
$\phi$ - полагается, внезапно, классической координатой (до этого момента), при квантовании становится оператором. Импульс определяется из лагранжиана и оказывается равным $\pi=\hbar N$ - тоже становится оператором.
Постулируется коммутационное соотношение $[\pi,\phi]=-i \hbar$. Строится гамильтониан и т.д. дальше все более или менее стандартно. Состояния, например, зарядового кубита ассоциируются с состояниями с различными $N$. Приводятся фотографии работающего кубита (это я к тому, что теория проверена и работает).

А теперь вопрос - почему это работает?
Вроде бы все стандартно. Квантовая теория постулируется, а не выводится из чего-либо (это чтоб не кидали в меня тапками).
В качестве подпорок для построения квантовой теории берется теория классическая, находится лагранжиан, "классическая координата", сопряженный импульс, гамильтониан; постулируется коммутационное соотношение между координатой и импульсом. И вперед. В конце концов проводятся эксперименты для доказательства, что это все не напрасно.
Но все же - почему это работает для такой сложной системы? Почему разность фаз куперовского конденсата безропотно играет роль классической координаты?
Не стоит ли за этим какой-то принцип, который сделал бы подобные построения менее удивительными?
(Я прочитал тему. «Нобелевка 2025: макроскопическое туннелирование в эл. цепях» Там есть кое-какие намеки касающиеся моего вопроса, но только намеки)

[amon]

naskamejke в сообщении #1717800 писал(а):

Но все же - почему это работает для такой сложной системы?

IMHO, потому, что авторы на кривой козе пытаются объехать уравнения Гинзбурга-Ландау. Обычно теория джозефсоновского перехода строится либо через введение туннельного гамильтониана в стандартную БКШ, как это сделал сам Джозефсон, либо через разложение свободной энергии по параметру порядка и условие минимума свободной энергии, дающее то самое уравнение Гинзбурга-Ландау для конденсатной волновой функции. Оба этих подхода не используют "квантование тока в конденсаторе". Почему последний подход дает такой-же ответ, я затрудняюсь ответить. Теория Джозефсоновского перехода описана во всех стандартных книжках про сверхпроводимость задолго до моды на кубиты, и, если интересно, лучше заглянуть в них.

[naskamejke]

Ну заглянул я в книги Буккеля, Тинкхама, немножко ЛЛ9. Везде теория заканчивается на уравнениях которые выше трактуются как классические (с усложнениями и приложениями, но не о них речь). У Тинкхама есть какой-то намек, но там какие-то совсем жуткие дебри чувствуются.
Вот книга Лихарева - не новая, но очень подробная. Там подход близкий к тому, что я описал (хотя о кубитах он не думал тогда).
Вот, говорите, на кривой козе. Но почему это все-таки работает, на козе-то? Ведь работает, не врут же.

[amon]

naskamejke в сообщении #1717832 писал(а):

Но почему это все-таки работает, на козе-то?

Потому, что уравнения Гинзбурга-Ландау чисто квантовые, но их, с точностью до численных значений коэффициентов, можно получить из общих соображений о разложении свободной энергии по параметру порядка. Микроскопика нужна только для получения этих самых численных значений, и если считать коэффициенты заданными, то результат можно получить для любой модели, для которой такое разложение работает. Возможно (я не проверял) это сработает и для модели для токов и конденсаторов. Мне это напоминает изучение физики в школе, когда дети нужной математики не знают, и им вместо нормальной теории подсовывают набор заклинаний, в который предлагается поверить. Для общего образования это, может, и годится, но если кто-то хочет всерьез разобраться, надо лезть в "жуткие дебри".

[Taus]

amon, уравнение Гинзбурга-Ландау ни в коем случае не квантовое, хотя и похоже на уравнения Шрёдингера. Производной по времени нет, а чтобы ввести её - ещё то дело обосновывать...

[amon]

Taus в сообщении #1718008 писал(а):

Производной по времени нет

Ох! Значит стационарное уравнение Шредингера тоже не квантовое! А мужики-то не знали... Гинзбург с Ландау исходно писали уравнение на "волновую функцию сверхпроводящих электронов" в равновесном состоянии - вещь сугубо квантовую. Это уравнение довольно просто переписывается и на нестационарные состояния.

[pppppppo_98]

amon в сообщении #1718021 писал(а):

Ох! Значит стационарное уравнение Шредингера тоже не квантовое! А мужики-то не знали... Гинзбург с Ландау исходно писали уравнение на "волновую функцию сверхпроводящих электронов" в равновесном состоянии - вещь сугубо квантовую. Это уравнение довольно просто переписывается и на нестационарные состояния.

Звыняюсь ... Но ваши оппоненты правы. Уравнение Ландау Гинзбурга только напоминают уравнения Шредингера. Во первых там нет времени, но это ладно во вторых они нелинейны по параметру корый почему то называется волновой функцией

[amon]

pppppppo_98 в сообщении #1718089 писал(а):

Уравнение Ландау Гинзбурга только напоминают уравнения Шредингера.

А я где-то сказал, что Гинзбург-Ландау выводится из уравнения Шредингера? По-моему, я писал, что это уравнение получается как условие минимума разложенной по комплексному параметру порядка свободной энергии. Квантовость таится в самом параметре порядка - он чисто квантовая вещь.

[Cos(x-pi/2)]

amon
Разумеется, возникновение сверхпроводящего конденсата - квантовое явление; для него есть микроскопическая квантовая теория (БКШ), и есть уравнение ГЛ для макроскопического параметра порядка $\psi,$ так что $\psi$ это квантовая вещь в данном смысле. Но тот факт, что комплексное поле $\psi$ это "точка" минимума свободной энергии, означает пренебрежение его квантовыми флуктуациями. (Упрощённая аналогия решению $\psi$ уравнения ГЛ: точка $x$ минимума потенциальной ямы $U(x)$ в классической механике частицы). В этом смысле уравнение ГЛ это уравнение классического, т.е. неквантованного поля $\psi.$ И в этом же смысле уравнения Джозефсона для разности фаз конденсатов и для энергии джозефсоновского контакта аналогичны уравнениям классической механики.

В работах о квантовых свойствах джозефсоновских контактов (и теоретических и экспериментальных, их уже очень много в связи с большой популярностью темы кубитов) не объезжаются на кривой козе уравнения ГЛ, а рассматриваются явления, которые уравнениями ГЛ и уравнениями Джозефсона не описываются - квантовая механика параметра порядка. (Аналогия: классическая механика не описывает квантование уровней энергии частицы в потенциальной яме $U(x)).$


naskamejke

naskamejke в сообщении #1717800 писал(а):

почему это работает для такой сложной системы? Почему разность фаз куперовского конденсата безропотно играет роль классической координаты?

Наверное это примерно такой же вопрос, как "а почему вообще работает квантовая механика - почему она применима к любой классической степени свободы в физике, вне зависимости от её природы?"

Никто не знает, почему законы природы именно такие; просто нам довелось оказаться в мире именно с такими законами физики.

В физике квантовая картина переходит в классическую (т.е. приближённо описывается как класическая), когда в системе очень много частиц, они обладают независимым поведением, и температура системы высокая. Эти факторы, образно говоря, - "враги" квантовой механики. В сверхпроводящем же конденсате электроны ведут себя не независимо, а скоррелированно - эта система описывается параметром порядка $\psi$, тепловой беспорядок при очень низкой температуре становится малым. Тем самым и возникают условия для проявления квантования степеней свободы, соответствующих параметру порядка (точнее говоря - разностям параметров в джозефсоновском контакте).

[naskamejke]

Я не ожидал прямого конкретного и окончательного ответа. Но мысли умных людей по данному вопросу мне были интересны. (Если что, я не считаю мой вопрос философским, сугубо физическим).
Пока что, я поинтересовался, что думает ИИ - простая бесплатная версия Gemini, и был приятно удивлен. (Само по себе это подозрительно. У меня небольшой опыт общения с ИИ, но до сих пор ответы на вопросы в областях, где я считаю себя профессионалом меня раздражали, хотя строго говоря не были неверными; общение же в областях где я дилетант было относительно приятным. Ну что ж, в области квантовой теории конденсированного вещества я более чем дилетант). Так вот, были и глюки и сомнительные утверждения и вещи которые я буду проверять по книгам. Но были и интересные мысли.
Например, квантование магнитного потока, как экспериментальный факт, намекает на то, что к фазе нужно относиться не как классической координате а как квантовой наблюдаемой.
Например, коммутационное соотношение между количеством пар на обкладках и разностью фаз связано с известным коммутационным соотношением между плотностью частиц и фазой. Причем более того, в этом последнем соотношении плотность частиц рассматривается как нетеровский ток симметрии (или заряд?), а симметрия - сдвиговая симметрия фазы. Для меня, как дилетанта, эта мысль была интересной, нужно подумать.
Обсуждалось также, что если строить квантовую механику по Фейнману (функциональные интегралы), то, с одной стороны правильность уравнений в классическом пределе обосновывает корректность выбора действия; с другой стороны, фейнмановская квантовая механика эквивалентна обычной операторной, отсюда корректность выбора наблюдаемых "координат и импульсов" (это я кратко и сумбурно резюмирую).
В общем, обсуждение с ИИ было довольно интересным. Не знаю только радоваться или печалиться по этому поводу.