Вряд ли по такой краткой "сопроводиловке к нобелевке" можно полностью разобраться в таких сложных экспериментальных работах, о которых идёт речь. Однако в ней даны ссылки на подробные публикации по этой теме, вот их и надо изучать (если эта тема Вам интересна), а также смотреть ссылки ещё и в указанных публикациях. Джозефсоника это сложная наука; если она Вам незнакома, а главную идею Вы уже уловили, - что, мол, речь идёт об открытии туннелирования состояния контакта, - то на этом можно бы и остановиться.
Величина

(так называемый критический ток джозефсоновского контакта) от температуры

не зависит; это техническая характеристика образца. Но есть нюанс: картина распределения плотности тока в джозефсоновском контакте сложным образом зависит от магнитного поля (потому что в сверхпроводниках есть эффект Мейсснера, так что достаточно слабое поле вытесняется из контакта, а сильное проникает в виде так называемых джозефсоновских вихрей, отчасти аналогичных вихрям Абрикосова в сверхпроводниках 2-го рода).
В результате оказывается, что критический ток контакта зависит от магнитного потока, проникшего в область контакта; критический ток контакта обращается в ноль, когда в контакт проникает целое число квантов магнитного потока. Получается, что в эксперименте можно регулировать (уменьшать) критический ток контакта

с помощью источника внешнего магнитного поля.
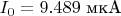
это критический ток джозефсоновского контакта с выключенным источником магнитного поля, а
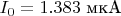
- с включенным.
Потенциал
("наклонённый косинус") имеет вид ям, отделённых друг от друга барьерами; рис. 2 в статье. Высота барьера

зависит от заданного тока

и от

Чем меньше у данного образца критический ток

тем ниже

С увеличением тока

через контакт барьер уменьшается и при

исчезает. А при
барьер есть; при этом в упоминавшейся выше чисто механической классической аналогии "координата"

должна покоиться на дне одной из потенциальных ям, и напряжение на контакте будет равно нулю:
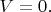
Но в реальных опытах имеют дело не с чистой механикой, а ещё и с тепловыми флуктуациями. Забудем временно про квантовое туннелирование:
При температуре

возможно классическое термоактивированное убегание "координаты"

из ямы - прыжок через вершину барьера. Вероятность этого убегания пропорциональна
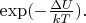
В опытах при заданной

подавали короткие импульсы увеличивающегося тока

и измеряли значения

при которых появлялось

(т.е. начиналось убегание

из ямы; дальше для краткости называю это просто "убеганием"). Чем ниже была температура образца

тем при больших значениях

возникало убегание. Понятно, почему это так: при понижении температуры вероятность термоактивированных прыжков через барьер заданной высоты уменьшается, и чтобы прыжки всё-таки становились опять вероятными, надо понижать высоту барьера
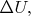
т.е. больше увеличивать
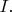
Авторы придумали специальный способ изображения измеренной вероятности убегания - некими формулами, в которые входят параметры образца и экспонента

Т.е. по измеренной при заданной

вероятности убегания вычислялась формальная величина

- "температура убегания", escape temperature.
При не слишком низких значениях

опыт дал значения
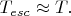
Авторы назвали эту ситуацию "классическим режимом".
В пределе с

в классической механике нет термоактивированных прыжков и, значит, не должно быть убегания. Т.е. при
вероятность убегания в классической картине при

стремится к нулю. С ней и найденная в опытах зависимость
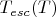
давала бы при экстраполяции к

значение
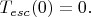
Теперь вспомним про туннелирование:
Квантовая механика, если она применима к такой макроскопической "координате", как

говорит: поскольку возможно туннельное проникновение сквозь барьер, то даже при

вероятность убегания не должна обратиться в ноль. Тогда и
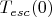
не должна обращаться в ноль. Эту ситуацию назвали "квантовым режимом". Это область таких низких температур

в которой при понижении температуры вероятность убегания перестаёт зависеть от температуры

и стремится к отличному от нуля значению из-за туннельного эффекта. При этом и график
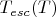
должен "выходить на полку" - стремиться к постоянному значению
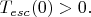
.
Существует теоретическая формула для оценки пограничной температуры, crossover temperature, ниже которой классический режим сменяется квантовым режимом. Для образца с
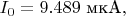
о котором идёт речь в статье, эта формула выдала значение температуры кроссовера

Существует теоретическая формула и для оценки
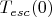
в квантовом режиме. В статье для образца с
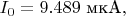
это значение равно
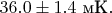
Экспериментальное значение

в квантовом режиме оказалось равным
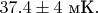
Оно хорошо согласуется с теоретическим предсказанием, этот факт и позволил авторам утверждать, что они обнаружили макроскопическое туннелирование.
Чтобы подтвердить этот вывод, т.е. убедиться, что ненулевая вероятность убегания при низкой температуре не вызвана какими-то классическими причинами, типа шумами (способными активировать надбарьерные прыжки), авторы повторили опыт в прежних экспериментальных условиях, но только понизили

внешним магнитным полем до значения
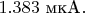
При этом температура кроссовера уменьшилась, стала равной
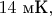
и классический режим (т.е. ход

соответственно продолжился до более низких температур по сравнению с первым опытом, в котором величина критического тока была больше. Значит, нет шумов, которые могли бы вызвать в первом опыте насыщение низкотемпературного значения
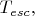
имитирующее квантовый режим с туннелированием.
В статье на рис. 3 показаны и прокомментированы зависимости
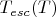
для обоих вариантов опыта. Термины "квантовый режим" и "классический режим" из оригинальной публикации авторов заменены в этой статье на "Quantum Junction" и "Classical Junction".