Диагональ в Канторовском методе

[Ximia]

Это, как я понимаю, само качество этого медота, что можно построить эту диагональ для счетного множества.

Интересно можно ли такую же диагональ построить проиднексировав последоватльность 0,1 несчетным множеством ?

[Mikhail_K]

Ximia в сообщении #1717191 писал(а):

Это, как я понимаю, само качество этого медота, что можно построить эту диагональ для счетного множества.

Фактически, в доказательстве теоремы Кантора такая диагональ как раз и строится (только не называется диагональю). 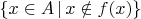Для любого отображения $f$ из множества $A$ (возможно несчётного) в множество его подмножеств (а подмножество можно интерпретировать как набор нулей и единиц, проиндексированный множеством $A$ - где стоят единицы, те элементы входят в подмножество) строится подмножество (то самое $\{x\in A\,|\,x\notin f(x)\}$ - для случая счётного $A$ это и будет диагональная последовательность: там где на диагонали $x\in f(x)$ и стоит $1$, те элементы не включаем в подмножество и ставим $0$, и наоборот), которое точно не равно никакому $f(y)$ для $y\in A$ (отсутствует в таблице).

[Ximia]

Спасибо за пояснение!