PadawanДа, примерно так как написал
B@R5uk. Сначала доказываем, что функция не дифференцируема в точках вида
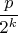
, для чего использовалось вот это свойство
Если g сплюснуть по x и по y в 2 раза, а потом к результату добавить h, то получится снова g.
Потом, для любой точки

не такого вида заключаем ее в набор сходящихся интервалов
![$\left[\dfrac{p_m}{2^m},\dfrac{p_m+1}{2^m} \right]$ $\left[\dfrac{p_m}{2^m},\dfrac{p_m+1}{2^m} \right]$](https://dxdy-02.korotkov.co.uk/f/d/b/b/dbb02cdee322507772ef5cb76feaeea282.png)
и доказываем, что последовательность
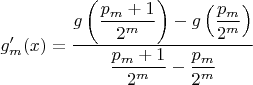
не является последовательностью Коши (т.к. разность соседних членов всегда равна

, т.е. наклону
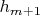
). Следовательно, и предела, который должен был быть равен производной в

- не существует.