Задача по ТЧ

[Shadow]

ex-math в сообщении #1717011 писал(а):

А разве случай $2p$ не покрывается первой частью рассуждения?

Наверное, просто для меня первая часть - поиск существования таких $n,x$ что

$\dfrac{(n-1)!}{x} \not \equiv 0 \pmod n$.

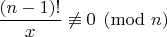
и лишь во второй части из найденных уже поиск второго условия. Не ожидал "гибрида". :)

bot в сообщении #1716963 писал(а):

Поэтому число $x$, должное быть сравнимым с произведением остальных по модулю $n$ делится на $p^k$.
Следовательно, из составных годными могут быть только $p^m$.

Попробую разобратся. Для выполнения вышеуказанного условия необходимо наличие хотя бы одного ростого $p$:

$v_p((n-1)!)-v_p(x)<v_p(n)$

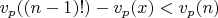
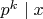
Тогда должно $p^k \mid x$. Также $p^k \mid n$

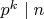
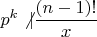
но при таких условиях $p^k \not | \dfrac{(n-1)!}{x}$ и уже сравнение (из второй части) не выполняется.

[ex-math]

Мы сразу ищем такой $x$, который будет сравним с $\frac{(n-1)!}x$ по модулю $n$, а значит по каждому модулю $p^k$. Поскольку $(n-1)!$ делится на $p^{2k-1}$, то одно из этих чисел точно делится на $p^k$, а значит делятся оба, поскольку они сравнимы. Получается, что $x$ делится на все $p^k$, то есть делится на $n$, что невозможно