колебания системы

[Most1k]

Найти собственную частоту малых колебаний системы, изображённой на рисунке, при одинаковом смещении грузов массой $m = 1 $кг в разные стороны. Каждый груз подвешен на жёсткую невесомую спицу длиной $l = 1 $ м. В положении равновесия пружины жесткостью $k =10 $Н/м не деформированы. Ускорение свободного падения принять равным 10 м/с2. Ответ выразите в с -1 и округлите до целых.


Пусть х1 и х2 это начальные удлинения нижних и верхнее пружин соответственно, тогда из уравнения моментов $x_2=2x_1$ /.
При отклонение шарика(и соответственно нижних пружин) на х верхняя пружина отклоняется на х/2 с каждой стороны из кинематических связей . полная энергия системы
(2k(x_1-x)^2)/2 + (k(x_2+x)^2)/2 + mv^2 = E

($\dot{x}$)^2 + (3kx^2)/2m +kx(x_2/2-x1)=Const

($\omega$)^2 = 3k/2m

$\nu$= $\sqrt{3k/2m}$$\cdot$1/2$\pi$
но ответ должен быть 5 с-1

[realeugene]

Most1k в сообщении #1714271 писал(а):

$(2k(x_1-x)^2)/2 + (k(x_2+x)^2)/2 + mv^2 = E$

Ваше уравнение не симметрично по $x_1$, $x_2$.А, вы так обозвали какие-то "начальные удлинения", которые по условию в состоянии равновесия равны нулю. И вы ещё не учитываете подъём грузов: они при отклонении поднимаются. Впрочем, требуемый ответ на самом деле странный.

[Most1k]

Да, я пересчитал с учетом потенциальной энергии, но у меня все равно не сходится .Выходит
$\omega=\sqrt{\frac{3kl+4mg}{2ml}}$
Вот уравнение
$kx^2+kx^2/2 + 2mgx^2/l + mv^2=E$

[Cos(x-pi/2)]

Most1k, какое-то непонятное уравнение Вы пишете. Должно быть два уравнения Ньютона - по одному на каждую степень свободы, т.е. по одному уравнению динамики для смещения каждого груза из положения равновесия. Соответственно, у этой механической системы получаются два типа собственных колебаний, каждое со своей собственной частотой.

Один тип колебаний (одна собственная мода) это когда грузы колеблются синфазно - с одинаковой амплитудой смещаются в одну и ту же сторону. Средняя пружина при этом "не работает", её жёсткость не даёт вклада в ответ. Второй тип колебаний (вторая собственная мода) - противофазные смещения грузов с одинаковой по абсолютной величине амплитудой. Средняя пружина при этом "работает", и поэтому частота получается более высокой - вот её и требуется найти по условию задачи.

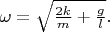
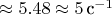
Всё это (типы колебаний и собственные частоты) автоматически получается из решения уравнений динамики. У меня получилось, что вторая частота (которая более высокая) равна $\omega =\sqrt{\frac{2k}{m}+\frac{g}{l}}.$ Численно это $\approx 5.48\approx 5\,\text{с}^{-1}$ без деления на $2\pi.$

P.S. UPD: это у меня ошибочная формула вышла, см. ниже исправление.

[realeugene]

Cos(x-pi/2) в сообщении #1714276 писал(а):

Численно это $\approx 5.48\approx 5\,\text{с}^{-1}$ без деления на $2\pi.$

Не писать радианы в секунду - путать людей. Хоть они и безразмерные, но всё же угловые величины. Герцы - это те же обратные секунды, только полных периодов в секунду.

[Cos(x-pi/2)]

Most1k
Прошу прощения, я сослепу ошибся. Теперь у меня получилось, что вторая частота (которая более высокая) равна $\omega =\sqrt{\frac{3k}{2m}+\frac{g}{l}}.$ Численно c данными из условия задачи это $ 5\,\text{с}^{-1}$ без деления на $2\pi.$ Most1k, у Вас почти такой же ответ, т.е. он у Вас в основном правильный; только с членом $g/l$ под корнем мы не сходимся (но я и тут мог ошибиться, надо будет на свежую голову завтра проверить :)

[wrest]

Cos(x-pi/2) в сообщении #1714281 писал(а):

но я и тут мог ошибиться, надо будет на свежую голову завтра проверить

Зависимость от $g/l$ должна быть: в пределе при отсутствии влияния пружин (к нулю стремится коэффициент упругости либо масса грузов стремится к бесконечности) должен получаться обычный математический маятник.

[Most1k]

Cos(x-pi/2)
Я неправильно выразил изменение потенциальной энергии , но теперь у меня получается ответ как у вас, так что полагаю, что он правильный

[Cos(x-pi/2)]

wrest

wrest в сообщении #1714283 писал(а):

в пределе при отсутствии влияния пружин (к нулю стремится коэффициент упругости либо масса грузов стремится к бесконечности) должен получаться обычный математический маятник.

Да, это хорошая проверка.

Most1k

Most1k в сообщении #1714301 писал(а):

теперь у меня получается ответ как у вас, так что полагаю, что он правильный

Ваш метод решения я понял. Да, он верный, поскольку в условии задачи сказано, для какой конкретно моды надо найти собственную частоту. Можно считать, что эта задача успешно решена.

[realeugene]

Половина верхней пружины имеет жёсткость $2k$, при переносе точки приложения силы вниз (в два раза большее смещение даёт половинную силу) эквивалентная жёсткость уменьшается в 4 раза и составляет $\frac k 2$, внизу она включена параллельно с левой пружиной жёткости $k$, при параллельном подключении жёсткости суммируются, так что это эквивалентно грузу массы $m$ на конце пружины жёсткостью $\frac 3 2 k$. Вот как интуитивно добавить маятник, уже непонятно.

[realeugene]

realeugene в сообщении #1714309 писал(а):

Вот как интуитивно добавить маятник, уже непонятно.

А впрочем, понятно. Подвес маятника длины $l$ эквивалентен горизонтальной пружине с жёсткостью $k_l=\frac{mg}l$: $\varphi=\frac x l$, $h = \frac {l \varphi^2}2$, $E = mgh = \frac{k_l x^2}2$.

Ну или же просто из совпадения частот колебаний $\frac m {k_l} = \frac l g$.

[Alex Krylov]

Кинетическая энергия системы:
$E=\frac{m (l \dot{\theta_1})^2}{2} + \frac{m (l \dot{\theta_2})^2}{2}$
Потенциальная энергия системы:
$U=\frac{k (\frac{l}{2}\sin(\theta_1)-\frac{l}{2}\sin(\theta_2))^2}{2} + \frac{k (l \sin(\theta_1))^2}{2} + \frac{k (l \sin(\theta_2))^2}{2} - m g l \cos(\theta_1) - m g l \cos(\theta_2)$
Лагранжиан:
$L = E - U$

Система двух дифф. уравнений:
$\left\{ \begin{array}{rcl} \frac{d}{dt}(\frac{\partial L}{\partial \dot{\theta_1}}) = \frac{\partial L}{\partial \theta_1} \\ \frac{d}{dt}(\frac{\partial L}{\partial \dot{\theta_2}}) = \frac{\partial L}{\partial \theta_2} \\ \end{array} \right$

После линеаризации правой части системы:
$\begin{bmatrix} \ddot{\theta_1} \\ \ddot{\theta_2} \end{bmatrix} = \begin{bmatrix} -\frac{g}{l}-\frac{5 k }{4 m} & \frac{k}{4 m}\\ \frac{k}{4 m} & -\frac{g}{l}-\frac{5 k }{4 m} \end{bmatrix} \begin{bmatrix} \theta_1 \\ \theta_2 \end{bmatrix}$

Далее ищем общее решение посредством (обратного) преобразования Лапласа:
$s^2 \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}\begin{bmatrix} \theta_1(s) \\ \theta_2(s) \end{bmatrix} - s \begin{bmatrix} \theta_{10} \\ \theta_{20} \end{bmatrix} = \begin{bmatrix} -\frac{g}{l}-\frac{5 k }{4 m} & \frac{k}{4 m}\\ \frac{k}{4 m} & -\frac{g}{l}-\frac{5 k }{4 m} \end{bmatrix} \begin{bmatrix} \theta_1(s) \\ \theta_2(s) \end{bmatrix}$

$\begin{bmatrix} \theta_1(s) \\ \theta_2(s) \end{bmatrix} = (s^2 \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} - \begin{bmatrix} -\frac{g}{l}-\frac{5 k }{4 m} & \frac{k}{4 m}\\ \frac{k}{4 m} & -\frac{g}{l}-\frac{5 k }{4 m} \end{bmatrix})^{-1} s \begin{bmatrix} \theta_{10} \\ \theta_{20} \end{bmatrix}$

Общее решение:
$\theta_{1,2}(t) = \frac{1}{2} [(\theta_{10}+\theta_{20})\cos(\sqrt{\frac{g}{l}+\frac{k}{m}} t) \pm (\theta_{10}-\theta_{20})\cos(\sqrt{\frac{g}{l}+\frac{3 k}{2 m}} t)]$

При $\theta_{20} = - \theta_{10}$
$\theta_{1,2}(t) = \pm \theta_{10} \cos(\sqrt{\frac{g}{l}+\frac{3 k}{2 m}} t) = \pm \theta_{10} \cos(5 t)$

[Alex Krylov]

Добавление к тому, что выше...

Изображения по Лапласу колебаний $\theta_{1}(t), \theta_{2}(t)$ имеют вот такой красивый вид:
$\theta_{1,2}(s) = \frac{(\theta_{10}+\theta_{20}) s}{2(s^2+\frac{g}{l} +\frac{k}{m})} \pm \frac{(\theta_{10}-\theta_{20}) s}{2(s^2+\frac{g}{l}+\frac{3 k}{2 m})}$
И полюсы тут сразу видны.

Как известно, для колебания вида $\exp(-\alpha t) \cos(\omega t + \varphi), \alpha>0$ его изображение по Лапласу равно:
$\frac{\cos(\varphi)(s+\alpha-\tg(\varphi)\omega)}{s^2+2 \alpha s +\alpha^2 +\omega^2}$

[Alex Krylov]

Ну и конечно вот эту систему можно сразу диагонализовать:
$\begin{bmatrix} \ddot{\theta_1} \\ \ddot{\theta_2} \end{bmatrix} = -\begin{bmatrix} \frac{g}{l}+\frac{5 k }{4 m} & -\frac{k}{4 m}\\ -\frac{k}{4 m} & \frac{g}{l}+\frac{5 k }{4 m} \end{bmatrix} \begin{bmatrix} \theta_1 \\ \theta_2 \end{bmatrix}$

$\frac{d^2}{dt^2} \theta=-A \theta = -V D V^T \theta \Rightarrow$
$\frac{d^2}{dt^2} \eta + D \eta = 0,\qquad \eta =V^T \theta,\quad\theta = V \eta$

И тогда искомые собственные частоты - это квадратные корни собственных значений матрицы $A$.

[pppppppo_98]

ИМХО... О стиле... у Крылова все абсолютно правильно, и все абсолютно верно алгортмизовано...Но... Если бы там было 5-6 степеней свободы я бы согласился с методикой... Но степеней свободы только 2. И из соображений симметрии Косинус абсолютно верно вывел обе степени свободы - почти устно. Симметрия сильно упрощает нахождение разделяемых переменных при анализе