Коллоквиум по (линейной) алгебре

[cxzbsdhwert]

Закончив слушать лекции (по №11) и семинары (Канунников и Тимашев (семинары записаны не в том же году что и лекции, и несколько отличаются, особенно Канунникова)) teach-in по первому модулю алгебре, провёл сам-себе коллоквиум по программе, но не по отдельным а сразу всем вопросам (почему-то думал что это займёт максимум час, а получилось 4 часа). Оцениваю на "между двойкой и тройкой" если строго, и "между тройкой и тройкой с плюсом" если более оптимистично.

К сожалению, в отличии от программы коллоквиума математического анализа, программа коллоквиума по алгебре не содержала задач. Из задач я решал в основном детские на семинарах по типу "приведите матрицу к улучшенному ступенчатому виду", "найдите определитель", и несколько по-солидней. Вчера решил задачу здесь не форуме: "доказать что существуют квадратные матрицы одинакового порядка, произведения которых в разной последовательности имеет разный ранг".


Не знаю насколько такая тема соответствует форуму, но хотел бы попросить заинтересованных пользователей позадавать теоретические вопросы и задачи, тем более, что насколько я понимаю среди пользователей форума есть штатные преподаватели ВУЗов. Поэтому, если Вы не устали от студентов формальных, буду благодарен за уделённое время студенту неформальному, тем более что данная тема особо дискуссии не предполагает - Вы даёте вопросы\задачи, я пытаюсь их решить.

Отмечу что по лекциям, модуль состоял исключительно из линейной алгебры. Алгебраические структуры, комплексные числа, многочлены - ничего этого не было. Задавать задачи на тригонометрию не стоит - я их сейчас не решу. Задачки типа разложения многочлена на множители ну разве что школьного уровня, хотя, повторюсь - модуль был целиком посвящён только линейной алгебре.

Программа коллоквиума

[Combat Zone]

Не совсем понятно, чего вы хотите. Если опроса по программе - она перед вами, воспроизводите в письменном виде и сверяйтесь.
Если задач на доказательство - берите любой учебник по линалу, например, Проскурякова, решайте. Там их много.

А еще гугл есть, туда можно вбить ваш запрос и получить сколько-то списков наподобие такого.https://disk.yandex.ru/i/bCddaw8phMtKdQ

Ваш ход, по идее, первый. Что вы решаете или на что пытаетесь ответить?

[cxzbsdhwert]

Combat Zone в сообщении #1714070 писал(а):

Не совсем понятно, чего вы хотите. Если опроса по программе - она перед вами, воспроизводите в письменном виде и сверяйтесь.
Если задач на доказательство - берите любой учебник по линалу, например, Проскурякова, решайте. Там их много.

А еще гугл есть, туда можно вбить ваш запрос и получить сколько-то списков наподобие такого.https://disk.yandex.ru/i/bCddaw8phMtKdQ

Ваш ход, по идее, первый. Что вы решаете или на что пытаетесь ответить?

Я не знаю насколько критично стоит оценивать свои ответы. Мне больше интересна теоретическая часть, поскольку действительно, задачи можно в задачниках порешать. Наверное же на зачёте студенту помимо явного перечня тем изложенного в программе коллоквиума задаются конкретные дополнительные вопросы, просится рассказать что-то что явно в программе не прописано, но подразумевается как подтема.
Было бы интересно на такие вопросы попробовать ответить.

За ссылку спасибо. Искать что-то типа "коллоквиум по алгебре" честно пробовал, но видимо не достаточно настойчиво.

И ещё не совсем понятно каким kpi лучше оценивать себя. Стоит ли вместо ответа по одной-двум темам из перечня коллоквиума\экзамена пытаться рассказать все от начала до конца, пытаться доказать все леммы и теоремы (что собственно и заняло больше четырёх часов подряд).

[nnosipov]

cxzbsdhwert в сообщении #1714055 писал(а):

Поэтому, если Вы не устали от студентов формальных, буду благодарен за уделённое время студенту неформальному, тем более что данная тема особо дискуссии не предполагает - Вы даёте вопросы\задачи, я пытаюсь их решить.

Я устал от всего, но все же предложу немного задач (моим студентам они до фени, но вдруг Вам захочется их порешать; я полагаю, что размышление над ними не принесет особого вреда, но насчет пользы не уверен, решать в любом случае Вам). Упоминаемые там задачники [1] и [2] --- это хорошо известные задачники Фаддеева&Соминского и Проскурякова.

Ха, хрен, не могу закачать на форум файл(

[Combat Zone]

cxzbsdhwert в сообщении #1714075 писал(а):

Было бы интересно на такие вопросы попробовать ответить.

Так и отвечайте. Выберите вопрос и отвечайте. Показательно, что в мой список вы даже не заглянули. Решите задачу 1 из приложения к списку, например.

nnosipov в сообщении #1714078 писал(а):

Ха, хрен, не могу закачать на форум файл(

Это необязательно. https://disk.yandex.ru/i/ul8wrbE4DOOv-w (Проскуряков)
Все ищется, ТС достаточно только предпринять усилия.

cxzbsdhwert в сообщении #1714075 писал(а):

Мне больше интересна теоретическая часть, поскольку действительно, задачи можно в задачниках порешать. Наверное же на зачёте студенту помимо явного перечня тем изложенного в программе коллоквиума задаются конкретные дополнительные вопросы, просится рассказать что-то что явно в программе не прописано, но подразумевается как подтема.

Я не понимаю, чем задача на доказательство свойств определителя в задачнике отличается от изложенного в лекции материала. Можно ведь считать, что этого материала не было. Кстати, определения определителя тоже разные. Ну и прочее.
В общем, "теоретический вопрос", по мне, это та же задача. Нет?

[cxzbsdhwert]

Combat Zone в сообщении #1714082 писал(а):

cxzbsdhwert в сообщении #1714075 писал(а):

Было бы интересно на такие вопросы попробовать ответить.

Так и отвечайте. Выберите вопрос и отвечайте. Показательно, что в мой список вы даже не заглянули. Решите задачу 1 из приложения к списку, например.

Почему? Открыл ознакомился, и даже тут же скачал. Вернулся сюда и поблагодарил.

Combat Zone в сообщении #1714082 писал(а):

Все ищется, ТС достаточно только предпринять усилия.

Да я просто наверное пытался найти программу коллоквиума с задачами именно по курсу который давал лектор, или за другие годы того же факультета.

Combat Zone в сообщении #1714082 писал(а):

Кстати, определения определителя тоже разные. Ну и прочее.В общем, "теоретический вопрос", по мне, это та же задача. Нет?

Ну в некотором смысле да. В общем, наверное программы которую Вы выслали, и которые я ещё нашёл наверное будет достаточно, может ещё nnosipov уточнит какие задачи Он имел в виду, попробую решить и буду двигаться дальше.

[Combat Zone]

cxzbsdhwert в сообщении #1714086 писал(а):

Почему? Открыл ознакомился, и даже тут же скачал. Вернулся сюда и поблагодарил.

Рассинхрон, стало быть )
Я реагирую на то, что было на момент написания. Вы тоже )

kpi тут вряд ли насоветуешь. Нормальный опрос можно устроить (на мой взгляд) исключительно в рамках старого доброго устного экзамена, а здесь вам не тут.
Но доказывать в рамках одного самоэкзамена материал всего курса не стоит.

[nnosipov]

Предлагаемые ниже задачи для самостоятельного решения относятся к следующим разделам курса алгебры: системы линейных уравнений, арифметические векторные пространства, матричная алгебра, теория определителей.

Уровень сложности задач в среднем несколько выше, чем у обычных упражнений на соответствующие темы (некоторые задачи вполне можно предлагать на студенческих олимпиадах). Впрочем, многие из этих задач читатель может найти в классических университетских задачниках [1] и [2], которые и рекомендуются в помощь.

В тексте без пояснений используются следующие обозначения: $\mathbb{Q}$, $\mathbb{R}$ и $\mathbb{C}$ --- поля рациональных, вещественных и комплексных чисел, $\mathbb{F}_q$ --- поле из $q$ элементов, $E$ и $O$ --- единичная и нулевая матрицы.

I. Системы линейных уравнений. Арифметические векторные пространства

1. В стаде $101$ корова. Если увести любую одну корову, то оставшихся можно разделить на две части по $50$ коров в каждой так, что суммарный вес коров первой части будет равен суммарному весу коров второй части. Докажите, что все коровы весят одинаково.

II. Матричная алгебра. Теория определителей

2. Докажите, что комплексный сточлен от ста переменных либо не имеет корней, все компоненты которых по модулю равны единице, либо имеет их бесконечно много. Примечание. Требуется знать, что такое комплексные числа.

3. В таблице из $11$ строк и $10$ столбцов написаны целые числа. Доказать, что можно вычеркнуть некоторые строки (не все, возможно, ни одной), после чего сумма чисел в каждом столбце будет четной.

4. Когда закончился хоккейный турнир (в один круг), оказалось, что для любой группы команд можно найти команду (может быть, из этой же группы), которая набрала нечетное число очков в играх с командами этой группы. Докажите, что в турнире участвовало четное число команд. (Поражение --- $0$ очков, ничья --- $1$ очко, выигрыш --- $2$ очка.)

5. Имеется набор из нескольких гирек. Если убрать из набора любую гирьку, то остальные можно разделить на две части так, что суммарный вес каждой части гирек будет одинаков. Докажите, что число гирек в наборе нечетно.

6. Докажите, что если

$$ \sum_{k=0}^lC_l^kx_k=a_l \quad (l=0,\,1,\,\dots,\,n), $$

то для $x_0$, $x_1$, ...., $x_n$ имеют место равенства

$$ x_j=(-1)^j\sum_{l=0}^j(-1)^lC_j^la_l \quad (j=0,\,1,\,\dots,\,n). $$

III. Основные алгебраические структуры

7. Сколько существует сюръективных отображений $f:X \to Y$, если $|X|=m$ и $|Y|=n$ ($m \geqslant n$)?

8. Какова средняя величина $|\Im{f}|$ для отображений $f:X \to Y$, если $|X|=m$ и $|Y|=n$ ($m \geqslant 0$, $n \geqslant 1$)?

[cxzbsdhwert]

nnosipov в сообщении #1714089 писал(а):

Предлагаемые ниже задачи для самостоятельного решения относятся к следующим разделам курса алгебры: системы линейных уравнений, арифметические векторные пространства, матричная алгебра, теория определителей.
1. В стаде $101$ корова

Нет, ну эту задачку разумеется давали на семинарах, я её через СЛУ и решил (хотя доказательство через СЛУ чисто формальное, безидейное)

-- 05.01.2026, 21:15 --

nnosipov в сообщении #1714089 писал(а):

3. В таблице из $11$ строк и $10$ столбцов написаны целые числа. Доказать, что можно вычеркнуть некоторые строки (не все, возможно, ни одной), после чего сумма чисел в каждом столбце будет четной.

Ну тут больше элементарная теория чисел сразу на ум приходит, а не попытка применить линейную алгебру:

(Оффтоп)

1. Сумма двух чётных чисел чётна
2. Сумма двух нечётных чисел чётна
3. Сумма чётного и нечётного числа нечётна
4. По п.3 сумма чётного числа нечётных чётна
5. По п.4 сумма любого числа чётных чётна - потому что любое чётное можно представить в виде произведения двоек, то есть сумм двоек; если слагаемых чётно, то их можно объединить в пары и тогда их сумма чётна по п.1; если их нечётно, тогда можно такую сумму можно обратно представить в виде произведения чётного на нечётное и снова представить в виде сумм, но уже не двоек в нечётном количестве, а некоторого нечётного числа в чётном количестве - их сумма чётна по п.2

Тогда, если в столбце из нечётного числа строк (11 например) убрать нечётное число, оставив чётное (например 10), то:
1. Либо они все чётные и тогда их сумма чётна по п.5
2. Либо они все нечётные и тогда их сумма чётна по п.4
3. Либо они частично чётны, частично нечётны, и поскольку их общее количество должно быть чётно то может быть так:
3.1 Чётное число чётных (сумма чётна по п.5) и чётное число нечётных (чётно по п.4). Тогда чётно+чётно=чётно
3.2 Нечётное чётных (чётно) и нечётных (нечётно). Чётное+нечётное=чётное.

Если же убрать чётное число строк, оставив нечётное (например не убирать вообще), то
1. Чётное число чётных (сумма чётна) и нечётное число нечётных (сумма нечётна). Сумма нечётна, значит уже не подходит, дальше можно не рассматривать.
2. Нечётное число чётных (сумма чётна) и чётное число чётных (сумма чётна). Сумма чётна

Может можно составить СЛУ с квадратной матрицей коэффициентов из чего как-то будет следовать, что компоненты вектора её решений всегда чётны. Компоненты же зависят от определителя. Хм, сейчас подумаю

[cxzbsdhwert]

nnosipov в сообщении #1714089 писал(а):

7. Сколько существует сюръективных отображений $f:X \to Y$, если $|X|=m$ и $|Y|=n$ ($m \geqslant n$)?

Групп и всего интересно ещё не было, но тут как я понимаю просто анализ и комбинаторика. Если под $|X|$ имеется в виду мощность, то сюръекций $mn$. Инъекций $m(m-1)(m-2)...(m-n+1)=\dfrac{m!}{(m-n)!}$; на число перестановок $n!$ не делим, поскольку порядок важен.
Если отображение понимается более шире чем функция, а именно одному элементу области определения могут соответствовать 2 и более элементов области значений, то сюръекций наверное существует $\dfrac{n^2+n}{2}mn$ или $n!mn$. Скорее первое.

[nnosipov]

cxzbsdhwert в сообщении #1714092 писал(а):

Ну тут больше элементарная теория чисел сразу на ум приходит, а не попытка применить линейную алгебру

Вы все-таки попытайтесь применить линейную алгебру (получите решение в одну строчку).

-- Вт янв 06, 2026 12:24:10 --

cxzbsdhwert в сообщении #1714101 писал(а):

Если под $|X|$ имеется в виду мощность,

Да, именно это.

cxzbsdhwert в сообщении #1714101 писал(а):

Если отображение понимается более шире чем функция,

Нет, не шире.

Ответ неверен.

-- Вт янв 06, 2026 12:29:25 --

cxzbsdhwert в сообщении #1714101 писал(а):

Инъекций $m(m-1)(m-2)...(m-n+1)=\dfrac{m!}{(m-n)!}$

Про инъекции вопроса не было, ибо ответ очевиден. Но у Вас он выписан неаккуратно (внимательно читайте условие задачи), хотя мыслите правильно.

[cxzbsdhwert]

nnosipov в сообщении #1714113 писал(а):

Ответ (про число сюръекций) неверен.

1. Рассмотрим сначала все инъекции из $m$ в $n$: сколько можно каждому образу однозначно сопоставить прообраз. Первому образу - один из $m$ прообразов, второму, после того как сопоставили первому - один из $m-1$ прообразов, и т.д. Получается $m(m-1)...(m-n+1)=\dfrac{m!}{(m-n)!}$
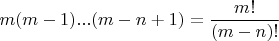
2. При каждой инъекции остаётся $m-n$ прообразов из $X$, которые и должны составить сюръекции.
3. Поскольку в отличии от однозначных сопоставлений, сюръективные могут отображаться в один образ, то первый из $m-n$ прообразов может отобразится в $n$ образов, на каждый из таких $n$ вариантов размещения первого прообраза приходится столько же - $n$ вариантов размещения второго прообраза, на каждую из вариаций из выборов первого и второго приходится по $n$ третьего и т.д.
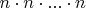
Тогда получается $n \cdot n \cdot ... \cdot n$ $m-n$ раз, т.е. $n^{m-n}$.
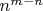
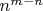
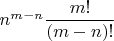
4. Ну и поскольку набор вариаций $n^{m-n}$ сюръективных сопоставлений приходится на каждую цепочку инъективных, то нужно умножать а не складывать, и в итоге получается $n^{m-n}\dfrac{m!}{(m-n)!}$ можно ещё $\dfrac{m!n^m}{(m-n)!n^n}$

nnosipov в сообщении #1714113 писал(а):

cxzbsdhwert в сообщении #1714092 писал(а):

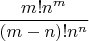
Ну тут больше элементарная теория чисел сразу на ум приходит, а не попытка применить линейную алгебру

Вы все-таки попытайтесь применить линейную алгебру (получите решение в одну строчку).

Во-первых я ошибся

cxzbsdhwert в сообщении #1714092 писал(а):

3.2 Нечётное чётных (чётно) и нечётных (нечётно). Чётное+нечётное=чётное.

(Оффтоп)

Сумма - нечётное, но это на самом деле не означает, при чётном числе оставшихся строк не всегда может быть чётная сумма, потому что можно просто по другому вычеркнуть - другую строку вычеркнуть. Но главное что я вообще не учёл, что во всех столбцах сумма должна быть чётной.
Рассуждать наверное стоило в обратную сторону, вычеркнув все кроме одной и дальше рассматривать сначала для первого столбца, дополнять строками если необходимо, потом для второго и теперь уже первого, то есть чтобы сумма и по первому и по второму была чётной, потом для третьего столбца и второго с первым и т.д., до последнего столбца. Правда по такому методу вроде может случится так что не хватит строк. Ну ладно

Как применить линейную алгебру, тем не менее, я не пойму:
1. Под исключением строк на основании того что было в курсе алгебры можно подвести только темы миноров и в некотором смысле эл.преобразования, когда вычитали пропорциональные строки зануляя одну.
2. Можно транспонировать всю таблицу 11 на 10, получим 10 столбцов в качестве строк. Тогда можно рассматривать СЛУ, нас как раз интересует сложение постолбоцово (построчно до транспонирования).
2.1 Столбец свободных членов наверное должен состоять из элементов вида $2x$, т.е. $(2b_1, 2b_2, ..., 2b_{10})$
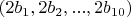
2.2 Дальше просто рассматривать СЛУ на совместность нельзя, поскольку нас интересует не любое решение а решение, компоненты которого либо $1$, либо $-1$ либо $0$, поскольку нас интересует чётность суммы элементов строк (столбцов до транспонирования) а при умножении на вектор решения только умножение на $1$ и $-1$ сохраняет чётность множителя. $0$ как раз означает что мы исключаем столбец/столбцы (строку/строки до транспонирования).
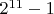
2.3 Ну и тогда остаётся $2^{11}-1$ (исключаем "все нули") вариаций решений: $(0,0,0,0,0,0,0,0,0,1),(0,0,0,0,0,0,0,0,1,0),(0,0,0,0,0,0,0,0,1,1),...,(1,1,1,1,1,1,1,1,1,1)$
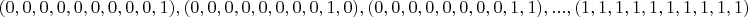
2.4 Если умножить транспонированную матрицу на матрицу $11$ на $2^{11}$, из вышеуказанных столбцов -всевозможных комбинаций исключения строк, то получим матрицу $10$ на $2^{11}$, каждый столбец которой это одна из всевозможных линейных комбинаций столбцов транспонированной матрицы (строк до транспонирования) с единичными или нулевыми коэффициентами (то есть с исключёнными столбцами (строками до транспонирования)).
Ну и вот каким-то образом нужно прийти к тому, что найдётся хотя бы один из $2^{11}$ столбцов все строки которого - чётные числа.
3. Ещё можно сказать про транспонированную матрицу (при условии, что не было нулевые строк), что СЛУ не определена, поскольку столбцов больше чем строк, то есть ранг транспонированной матрицы меньше числа столбцов (по основной лемме о линейной зависимости).
3.1 Применять критерий совместимости Кронекера-Капелли не получится, поскольку рассматривая произвольную матрицу ничего кроме того что написано сверху о её ранге нельзя утверждать, да и как уже написано даже если мы узнаем что СЛУ совместна, не всякое решение нас интересует.
4. Как-то пытаться применять метод Гаусса тоже не получится из-за произвольности матрицы.

5. Определитель даёт произвольное решение но не для произвольной матрицы, а только лишь квадратной да ещё и невырожденной, что опять-таки нарушает общность условия. Ну ладно, допустим мы рассматриваем 11 квадратных матриц 10 на 10, у которых вычеркнут один из столбцов (строка до транспонирования).
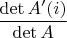
5.1 По формуле Крамера, $i$-ая компонента решения определённой СЛУ равна $\dfrac{\det A'(i)}{\det A}$, нам нужно чтобы это отношение было либо $1$ либо $-1$ либо ноль для всех $i$. Тогда определители должны быть равны по модулю, либо верхний должен быть нулевым.
5.2 Матрица определителя в числителе - это матрица коэффициентов с замененным $i$-ым столбцом на столбец свободных членов, которые все вида $2x$. Можно было бы компоненты столбца свободных членов представлять явно как сумму элементов, и тогда что-то говорить о чётности решения, но некоторые из слагаемых компонент столбца свободных членов могут отсутствовать чтобы равенство выполнялось, ну и тогда только наверное вводить параметры ещё. Короче не вариант
5.3 Если при замене вместо $i$-го столбца верхний определитель стал равен нулю, то значит без $i$-го столбца (строки до транспонирования) столбец свободных членов линейной выражается через остальные столбцы (строки до транспонирования). Правда опять-таки, линейной комбинацией с единичными или другими коэффициентами выражается не ясно.
Если верхний определитель после замены не равен нулю, значит без этого столбца столбец свободных членов не выражается через остальные, тогда такой столбец (строку до транспонирования) нужно оставить, то есть соответствующая компонента решения нулевой не должна быть.
Но нужно быть уверенным что верхний определитель если не равен нулю то по модулю равен нижнему.
Тогда, в принципе можно прийти к заключению, что существуют вектора решений (но опять-таки, при условии что матрица невырожденна, а задача явно, вне контекста определителей верна и для вырожденных матриц) имеющие все компоненты либо ноль либо один (минус один), при таком столбце свободных членов, ну что собственно и означает что "всегда" можно вычеркнуть строки так, что сумма элементов по всем столбца (до транспонирования) была бы чётна.
6. Ещё есть разложение определителя по столбцу
7. Чётность ещё фигурировала в перестановках, но не знаю как это применить, ну по крайней мере так, чтобы это было линейной алгеброй, а не, опять-таки теорией чисел.
8. Может-быть след матрицы как-то можно применить, не знаю
9. Может как-то ФСР СЛУ из такой матрицы как-то рассмотреть

Хотя бы одно из направлений мыслей было верным? Или вообще всё "не туда"?

[nnosipov]

cxzbsdhwert
Пардон, я морально не готов обрабатывать сейчас такую стену текста. Давайте я просто намекну, куда копать: в сторону утверждения "в $n$-мерном пространстве любая система, в которой больше $n$ векторов, является линейно зависимой".

Да, векторные пространства в приличных учебных заведениях рассматриваются сразу над произвольным полем скаляров.

[cxzbsdhwert]

nnosipov
А по числу сюръекций? Если коротко, то получилось $n^{m-n}\dfrac{m!}{(m-n)!}$

[nnosipov]

cxzbsdhwert
Неверно, там нет простой формулы. И вообще, решайте задачи подряд.

Я предупреждал, что задачи повышенной сложности.