Да, векторные пространства в приличных учебных заведениях рассматриваются сразу над произвольным полем скаляров.
В учебнике Винберга, по которому, как я понимаю читались лекции тоже сначала даются алгебраические структуры, да и на опубликованных семинарах, которые, правда, за другой год.
Более того, там ещё
сначала даётся теория определителей, в других учебниках даже вроде только затем векторные пространства, и только потом метод Гаусса.
Вам как преподавателю наверное с опытом виднее, но для меня, по крайней мере в первый раз это всё изучающему в той последовательности которую изложил Лектор, было удивительно, что вообще излагаться моглось как-то иначе.
Например, изучая материал в такой последовательности, я за долго до теоремы Крамера (которая вообще последняя лекция), после лекций про ранг предвосхитил критерий совместимости-определённости отличный от Кронекера-Капелли, а именно что СЛУ совместна если ранг её матрицы коэффициентов (столбцовый в частности) равен числу строк, а число столбцов больше либо равно числу строк; в частности, если число строк равно числу столбцов (и равно рангу) то СЛУ ещё и определена. Я даже хотел здесь задать вопрос, но дошёл черёд лекции по теореме Крамера.
Так что не знаю, по-моему материал даётся естественно.
-- 09.01.2026, 20:57 --Combat ZoneНе подскажите, в задаче "Элементы матрицы равны

. Доказать, что ее определитель – число четное." из программы которую Вы выслали решение такое? :
(Оффтоп)
В определителе факториал слагаемых, факториал всегда чётен. Слагаемых половина с плюсом половина с минусом (по теореме о том что в множестве перестановок половина чётных половина нечётных), но слагаемые - произведения единиц или минус единиц, обе, которые, тем менее нечётны. И тогда получается чётная сумма-разность нечётных, а это сумма чётного числа нечётных - чётна
И задача 8 пункт а) там только показать что определитель будет суммой алгебраических дополнений
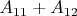
или нужно дальше копать?